zenterix
- 774
- 84
- Homework Statement
- I'm doing all the problems in Calculus by Spivak. I am on problem 3 of chapter 5 on Limits, and some of the items don't have solutions. I am interested in two particular items of this problem, ##vii## and ##viii##
- Relevant Equations
- We are asked to determine the limit ##l## for the given function and value of ##a##, and to prove that it is the limit by showing how to find a ##\delta## such that ##|f(x)-l|<\epsilon## for all ##x## satisfying ##0<|x-a|<\delta##.
The solution for this problem is not available in the solution manual.
Consider item ##vii##, which specifies the function ##f(x)=\sqrt{|x|}## with ##a=0##
Case 1: ##\forall \epsilon: 0<\epsilon<1##
$$\implies \epsilon^2<\epsilon<1$$
$$|x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$
Case 2: ##\forall \epsilon: 1\leq \epsilon < \infty##
$$\epsilon\leq\epsilon^2 \implies |x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$
Therefore
$$\forall \epsilon>0,|x-0|<\epsilon^2\implies|\sqrt{|x|}-0|<\epsilon$$
$$\implies \lim_\limits{x\to a} \sqrt{|x|}=0$$
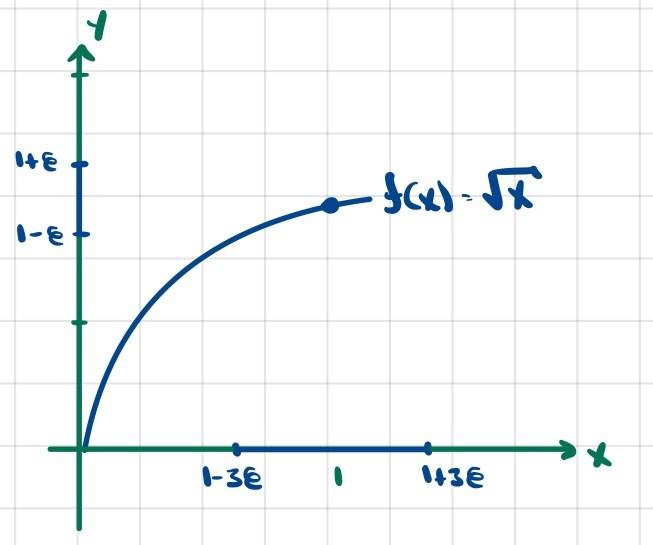
Is this correct?Now consider item ##viii##, which specifies the function ##f(x)=\sqrt{x}## near ##x=1##
$$|x-1|=|(\sqrt{x})^2-1^2|=|(\sqrt{x}+1)(\sqrt{x}-1)|\leq|\sqrt{x}+1||\sqrt{x}-1|$$
Assume ##|\sqrt{x}-1|<1##
$$\iff -1<\sqrt{x}-1<1\implies 1<\sqrt{x}+1<3$$
$$\iff |\sqrt{x}+1|<3$$
$$\iff |x-1|<3|\sqrt{x}-1|<3\epsilon$$
In words: Assume that ##f(x)## is less than 1 unit away from the value ##1##. From this follows that ##|x-1|<3|\sqrt{x}-1|<3\epsilon##. However, because all the steps involved an ##\iff##, we could actually start from assuming ##|x-1|<3|\sqrt{x}-1|<3\epsilon## and reach ##|\sqrt{x}-1|<1##.
In any case the conclusion is that
$$\forall \epsilon>0,|x-1|<3\epsilon\implies |\sqrt{x}-1|<min(1,\epsilon)<\epsilon$$
$$\implies \lim_\limits{x \to 1}\sqrt{x}=1$$
Is this correct?
Case 1: ##\forall \epsilon: 0<\epsilon<1##
$$\implies \epsilon^2<\epsilon<1$$
$$|x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$
Case 2: ##\forall \epsilon: 1\leq \epsilon < \infty##
$$\epsilon\leq\epsilon^2 \implies |x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$
Therefore
$$\forall \epsilon>0,|x-0|<\epsilon^2\implies|\sqrt{|x|}-0|<\epsilon$$
$$\implies \lim_\limits{x\to a} \sqrt{|x|}=0$$
Is this correct?Now consider item ##viii##, which specifies the function ##f(x)=\sqrt{x}## near ##x=1##
$$|x-1|=|(\sqrt{x})^2-1^2|=|(\sqrt{x}+1)(\sqrt{x}-1)|\leq|\sqrt{x}+1||\sqrt{x}-1|$$
Assume ##|\sqrt{x}-1|<1##
$$\iff -1<\sqrt{x}-1<1\implies 1<\sqrt{x}+1<3$$
$$\iff |\sqrt{x}+1|<3$$
$$\iff |x-1|<3|\sqrt{x}-1|<3\epsilon$$
In words: Assume that ##f(x)## is less than 1 unit away from the value ##1##. From this follows that ##|x-1|<3|\sqrt{x}-1|<3\epsilon##. However, because all the steps involved an ##\iff##, we could actually start from assuming ##|x-1|<3|\sqrt{x}-1|<3\epsilon## and reach ##|\sqrt{x}-1|<1##.
In any case the conclusion is that
$$\forall \epsilon>0,|x-1|<3\epsilon\implies |\sqrt{x}-1|<min(1,\epsilon)<\epsilon$$
$$\implies \lim_\limits{x \to 1}\sqrt{x}=1$$
Is this correct?