Spotting Errors in Transverse & Longitudinal Accelerations

Click For Summary
SUMMARY

The discussion focuses on the decomposition of acceleration vectors into longitudinal and transverse components based on a particle's velocity. The user derived the x-components of both acceleration vectors using the dot product and applied relativistic mass factors, specifically gamma and gamma cube. An error was identified in the formulation of the second equation, where the user mistakenly divided by gamma cube instead of multiplying. This correction is crucial for achieving equivalence between the derived equations.

PREREQUISITES
  • Understanding of vector decomposition in physics
  • Familiarity with the dot product and its applications
  • Knowledge of relativistic mass concepts, specifically gamma factors
  • Basic principles of 3-momentum and its differentiation
NEXT STEPS
  • Study the derivation of 4-acceleration in special relativity
  • Learn about the implications of relativistic mass on force calculations
  • Explore vector calculus applications in physics
  • Review advanced topics in momentum conservation in relativistic contexts
USEFUL FOR

Physics students, researchers in relativistic mechanics, and anyone involved in advanced dynamics and kinematics analysis.

greswd
Messages
764
Reaction score
20
Let's say you know all 3 cartesian components of a particle's velocity and all 3 for it's acceleration.

You can split the acceleration vector into two vectors, one parallel (longitudinal) to the velocity vector and one perpendicular (transverse) to the velocity vector.

Then, I found the x-components of both acceleration vectors in terms of the 6 variables listed at the start. That would be the component of each acceleration vector parallel to the x-axis. I used the dot product to derive it.

As you can see below, I multiplied the transverse-x acceleration component by gamma and the longitudinal-x acceleration component by gamma cube. These are the formulas for the longitudinal and transverse masses.

I can get a formula for the x-component of the Force.
errors.png
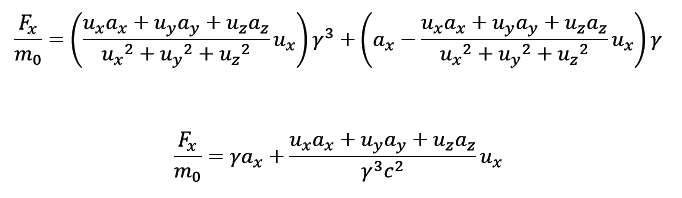In order to get the second formula, I differentiated the x-component of the 3-momentum with respect to time.
I expected both equations to be equivalent, but try as I might, I can't make them equal.Can you help me spot the error(s) in my formulas?
 
Physics news on Phys.org
Sorry, it didn't help me at all.

Anyway, I've discovered my careless mistake. It is supposed to be multiplied, not divided, by gamma cube for the second equation.
 

Similar threads

Graduate Gravitational Waves-Longitudinal or transverse
  • · Replies 1 ·
Replies
1
Views
3K
Undergrad What is the role of the longitudinal rapidity in relativistic contexts?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate General equation for hyperbolic motion in a 2D plane -- Help needed please
  • · Replies 14 ·
Replies
14
Views
2K
Undergrad Transverse inertial motion of rockets in acceleration
  • · Replies 18 ·
Replies
18
Views
2K
Undergrad Understanding Relation of Proper & Vector Quantities
  • · Replies 23 ·
Replies
23
Views
2K
Graduate Weyl tensor and coordinate acceleration
  • · Replies 12 ·
Replies
12
Views
3K
Undergrad In NMR, Why does longitudinal magnetization decrease when....
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Momentary Co-Moving Reference Frame in SR
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Relating orthogonal accelerations in special relativity
  • · Replies 1 ·
Replies
1
Views
1K
Graduate Is parallel transport exactly norm-preserving or only approximately?
  • · Replies 21 ·
Replies
21
Views
1K