SUMMARY
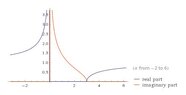
The discussion centers on the mathematical expression \(\sqrt{\frac{x-3}{x}} = \frac{\sqrt{x-3}}{\sqrt{x}}\), which holds true for \(x \in [3, \infty)\). Participants emphasize the importance of understanding domain restrictions, particularly that \(\frac{x-3}{x} \geq 0\) leads to valid solutions only in the specified range. The conversation highlights the distinction between real and complex numbers, particularly when evaluating functions like \(f(x) = \frac{\sqrt{x-3}}{\sqrt{x}}\) at values outside the domain, such as \(x = -1\).
PREREQUISITES
- Understanding of square roots and their properties
- Knowledge of domain restrictions in rational expressions
- Familiarity with complex numbers and their implications
- Basic algebraic manipulation skills
NEXT STEPS
- Study the properties of square roots in rational expressions
- Learn about domain restrictions in functions
- Explore complex numbers and their applications in algebra
- Investigate how to handle piecewise functions in mathematics
USEFUL FOR
High school mathematics teachers, students in advanced algebra courses, and anyone seeking to deepen their understanding of square roots and domain issues in rational functions.