Standing Vertical Jump physics problem

[Whatupdoc]

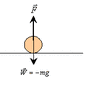
A Standing Vertical Jump. Basketball player Darrell Griffith is on record as attaining a standing vertical jump of 1.2 m (4 ft). (This means that he moved upward by 1.2 m after his feet left the floor.) Griffith weighed 890 N (200 lb).

1.) Use Newton's laws and the results of part (B) to calculate the average force he applied to the ground. F= m*a

ok i really don't know how to do this. i know that there is a force of 890 N that is already given. and the acceleration that i found from part b, which is below. if i plugged it in, i would find the mass, which is useless(i think).
can someone point me to the right direction? just a guess, but i just think it's 890N cause that's the force that he has.

this is part b.) If the time of the part of the jump before his feet left the floor was 0.300 s, what was the magnitude of his average acceleration while he was pushing against the floor? Results of part b is 16.2 m/s^2

 

[Leong]

<br /> \begin{multline*}<br /> \begin{split}<br /> &amp;Newton&#039;s\ 2nd\ Law\\<br /> &amp;\sum \vec{F}=m\vec{a}\\<br /> &amp;\vec{F}+\vec{W}=m\vec{a}\\<br /> &amp;\vec{F}=m\vec{a}-\vec{W}\\<br /> &amp;\vec{F}=m\vec{a}-(-mg)\\<br /> &amp;\vec{F}=m(16.2 + g)\\<br /> \end{split}<br /> \end{multline*}<br />

 

[M98Ranger]

To calculate the average force that Griffith applied to the ground, we need to use Newton's Second Law, which states that force is equal to mass times acceleration (F=ma). We already know the mass of Griffith, which is 200 lb or 890 N. Now, we need to find the acceleration that he experienced while pushing against the ground during the jump. This can be found by using the equation for average acceleration, which is a=Δv/Δt, where Δv is the change in velocity and Δt is the time interval. In this case, we know the change in velocity, which is the height of the jump, 1.2 m, and the time interval, 0.300 s. Therefore, the average acceleration experienced by Griffith is 1.2 m/0.300 s = 4 m/s^2.

Now, we can plug this value into the equation F=ma to calculate the average force applied by Griffith to the ground. This gives us F=890 N * 4 m/s^2 = 3560 N. Therefore, the average force that Griffith applied to the ground during his standing vertical jump was 3560 N. This shows the amount of force and power that professional basketball players like Griffith possess.