Builder89
- 28
- 0
Thanks everyone for the help. I think I'm good to go now. :-)
This discussion focuses on calculating the vertical forces acting on a bicycle's suspension system, specifically the force applied to the shock absorber when the bike is at rest and when it impacts the ground after falling. The user calculates the upward force on the rear axle based on a total bike and rider weight of 100 kg, determining that the vertical force at rest is 588 N and increases to 1176 N after a 1m fall. The conversation emphasizes the importance of distinguishing between force and energy, clarifying that the kinetic energy (mgh) should not be directly added to the static weight force when calculating the impact force on the suspension system.
PREREQUISITESMechanical engineers, bicycle designers, and enthusiasts interested in optimizing bicycle suspension systems and understanding the physics of impact forces.
OK, but I'd like to be confident you are calculating the torques correctly: ##\tau = Fr\sin(\theta)##Builder89 said:Thanks everyone for the help. I think I'm good to go now. :-)
Builder89 said:FR(cos12)(495) = FM(cos12)(102)
No, you have to treat FR and FS as two forces acting at different angles on the arm, balancing:Builder89 said:The force into the shock, FS = cos40(458.60)
Actually I was a bit wrong, but not in the way you think.Builder89 said:Hmmm, really? I feel you're wrong. FL is the pivot point, O. FM and FR are torque forces working to twist around FL in opposite directions.
Because part of the compression force on the shock comes from the reaction force at the pivot.Builder89 said:why can't I get the same FS using the following?
Sure, but that is just the vertical component of FS.Builder89 said:why can't FM be isolated as output from the swing arm diagram and fed into some other mechanism after the fact as a vertical force?
I think you mean FR, not FM.JBA said:FS = 495/102 * FM * cos 12 / cos 52° = 7.71 FM
But:haruspex said:FS cos 40 = FM
In your diagram in post #39, there are three forces acting where the shock meets the arm: FS, FM and the compression in the arm. You seem to be resolving in the direction parallel to the shock, but if you do that you must include the compression in the arm. Simpler to resolve normal to the arm.Builder89 said:cos(theta) = adj/hyp.
Why?Builder89 said:I'm trying to find the FM
This is what I have tried to explain in posts #42 and #45.Builder89 said:Apparently my method is wrong so I'm trying to understand why
haruspex said:FS cos(52) (102)=FR cos(12) (495).
So FS=7.7 FR.
In the drop scenario, you cannot compute FM independently of the shock behaviour.Builder89 said:How do I do the same thing for the linkage triangle in post 46? I'm not sure where to start to get FM.
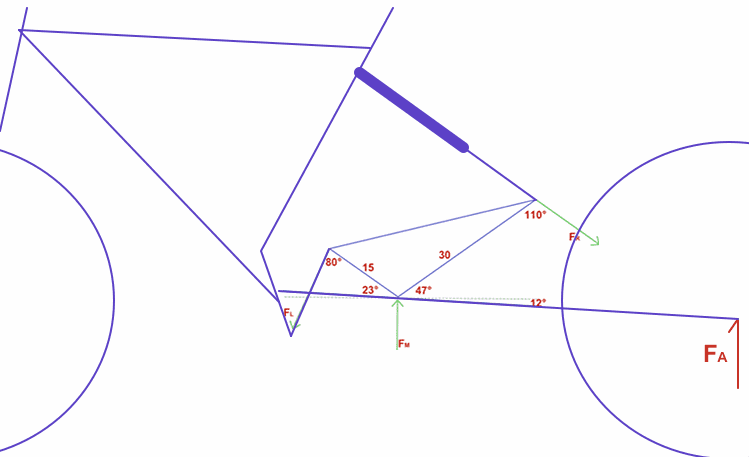
I believe your force diagram for the linkage in post #46 is wrong. (If correct it would be overspecified, with two unknowns, the magnitudes of the two forces, but three equations.)Builder89 said:Here is a rough representation of the context it goes in. All points on the triangle are pivots. FL is a rod attached to the frame on the bottom via another pin (pivot). The shock is only connected at the right point on the triangle and the frame up and left. Remember, we are doing the calculation in equilibrium at this point with the shock compressed 76mm. As such, this is how it looks. All numbers are mm.
And, as stated before, the FA is just the portion of weight on the bike that is at the rear tire.