- #1
Bodine1187
I am sizing a linear actuator to build a BMX gate. Please see the drawing below. I have a metal gate that is 20" tall and 9.5' wide. It will be steel and weigh approximately 150lbs.
I am mounting the rear of the linear actuator on a clevis 8" off the ground. The front will be mounted with another clevis 6" above the pivot point of the gate. I am trying to understand the amount of force I need to pull the gate up into a position perpendicular to where the bikes sit on the platform. The actuator length, fully extended will be 24.25". The force used to pull the gate into a perpendicular position will be at a 19.26-degree angle to the gate.
I've also included a picture of a bmx gate to give a better idea of what I'm building. I am only building the moving gate in the front, not the platform piece.
I do understand that the force needed will decrease as the gate moves through its motion, but I'm just worried about the gate force needed to start the motion.


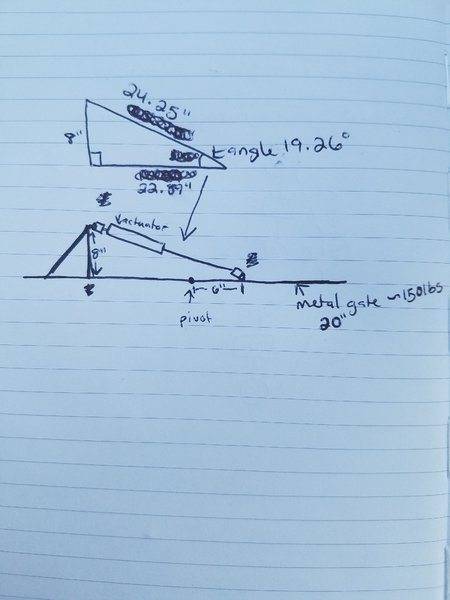
I am mounting the rear of the linear actuator on a clevis 8" off the ground. The front will be mounted with another clevis 6" above the pivot point of the gate. I am trying to understand the amount of force I need to pull the gate up into a position perpendicular to where the bikes sit on the platform. The actuator length, fully extended will be 24.25". The force used to pull the gate into a perpendicular position will be at a 19.26-degree angle to the gate.
I've also included a picture of a bmx gate to give a better idea of what I'm building. I am only building the moving gate in the front, not the platform piece.
I do understand that the force needed will decrease as the gate moves through its motion, but I'm just worried about the gate force needed to start the motion.