State Space Model of an RL Circuit

[YoshiMoshi]

Homework Statement

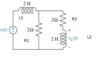
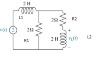
For the given circuits, identify state variables and derive a state-space model for each.
Assume the input is v(t) and the output is vL(t).

Homework Equations

The Attempt at a Solution

[/B]
So my issue is that I solved this problem using two different methods. First method I used was trying to find the state space model directly using KCL in the time domain. I then took my state space model used derived using this method and found the transfer function. I then found the transfer function directly using mesh analysis. For some reason I got two different transfer functions. So that means either my state space analysis from my first method was incorrect, or the second transfer function I found using mesh analysis was incorrect. I'm not exactly sure what I did was incorrect, my transfer function using mesh analysis, or my state space analysis. Any help would be greatly appreciated.

 

[berkeman]

The form of your answer using the 2nd method looks correct (bandpass filter), but I didn't check the math in detail

But it seems like you dropped a V(t) term in you answer using the first time-domain method? (Or I could be missing something)...