C268
- 26
- 0
1. Homework Statement :
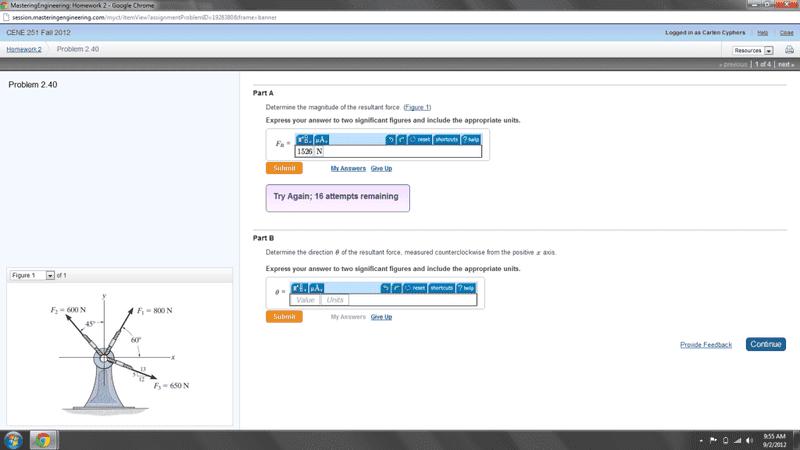
I keep attempting this problem and so far I have got this:
F1x: 150
F1y:260
F2x:424
F2y:424
F3x:600
F3y:250
Then I add the x's together and y's together, square both and take the square root for magnitude, but can't seem to get the right answer
The Attempt at a Solution
I keep attempting this problem and so far I have got this:
F1x: 150
F1y:260
F2x:424
F2y:424
F3x:600
F3y:250
Then I add the x's together and y's together, square both and take the square root for magnitude, but can't seem to get the right answer