Statics: load supported on a wooden frame

[SoylentBlue]

Homework Statement

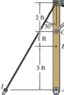
Given the frame shown, determine the internal loadings at D

Homework Equations

The Attempt at a Solution

This should be a simple problem...but I cannot see where I am making a mistake.
If I approach it by examining the entire structure, I get a wrong answer:

ΣFx: Ax + (cos60)IB = 0
ΣFy: Ay - (sin60)IB – 150 = 0
ΣM about I I: 3.44Ay – (7.44)(150) = 0

The 3.44 comes from determining, by trig, that IA is 3.44; the 150LB load is therefore 7.44 ft away from I

This yields Ay = 324.4
Plug back into sum of forces in y-direction; that yields IB = -201

OK now examine the section BDHC:
ΣFx: -(cos60)(201) + (cos45)GH=0
This yields GH= 142, which is wrong.
___________________

However, if I start instead with just the structure BDHC, I get:
sum of moments about B: (2)[(sin45)GH] – (4)(150)=0 then GH=424 which agrees with the book

Where did I make a wrong turn? Any help greatly appreciated. Thank you.

[/B]

 

[haruspex]

ΣFx: Ax + (cos60)IB = 0

Which way is the tension IB acting on the system? Have you been consistent with signs?

 

[SoylentBlue]

IB would have to be in tension. So at point I, Ix is to the left, and Iy is negative.

Oh, I see your point. Let's amend the equation:
ΣFx: Ax - (cos60)IB = 0
However, for the Fy equation, which is where we determine the value of Ay, the signs and logic and values are correct, right?
I assume Ay goes up, and AB is in compression. Obviously, the load goes down. And IB is in tension, so Iy goes down.

Small typo I just noticed...this should read:
ΣM about point I: 3.44Ay – (7.44)(150) = 0

Thank you for helping...I am trying to work through this course on my own, so the Internet is my instructor!

 

[haruspex]

This yields Ay = 324.4
Plug back into sum of forces in y-direction; that yields IB = -201

Try that step again. I get a positive IB (as it should be).

 

[SoylentBlue]

Now that was an embarrassing error. OK, I now have the correct answer for IB.

Next, we look at the top of the frame, examining DHC; If we sum the moments from point D, the moment caused by GH balances the moment caused by the load at point C, and we get the correct answer for the value of GH. So far so good.

However, shouldn't we also be able to look at BDHC, and sum all the forces in either the x or y direction? If we look at the y direction, in that case we get an incorrect value of zero for GH.
ΣFy: Ay - (cos30)(IB) + (cos45)(GH) -150=0
Ay is in compression, pushing up; IB is in tension pulling down, GH is pushing up, and of course the 150 load pulls down.
324 - 174+.707GH-150=0
324-324 = .707GH

This has to be an error in logic rather than a math error, right?

 

[haruspex]

If we sum the moments from point D, the moment caused by GH balances the moment caused by the load at point C

I assume you meant moments about B.

Ay - (cos30)(IB) + (cos45)(GH)

You are double counting.
The vertical force in AB is not the same all the way up. The force at A includes a component to balance the vertical load at G from GH. The force in AB at B does not include this. If your Ay is the force at A then you should not add a contribution from GH at H.