Statics - Support Reaction in Truss

[Philippe]

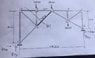
Homework Statement

I'm having a hard time finding the support reactions R_{fx} ; R_{fy} ; R_{kx} ; R_{ky} in this truss.

2. The attempt at a solution

I got four equations using the equilibrium conditions (sum of forces along x and y ; sum of moments on F and on C) but the system doesn't seem to have a solution. Am i missing something?

<br /> (\Sigma x = 0) R_{fx} + R_{ky} = 0 \\<br /> (\Sigma y = 0) R_{fy} + R_{ky} = 530 \\<br /> (\Sigma M_{f} = 0) -8R_{kx} + 40R_{ky} = 11100 \\<br /> (\Sigma M_{c} = 0) -20R_{fx} + 20R_{fy} -12 R_{kx} - 20R_{ky} = -500<br />

Thanks!

 

[haruspex]

You have treated the whole girder system as a single rigid structure. That means there are only three independent equations available. Any further you write down, whether linear forces or moments, can be deduced from those three.

Is it a single rigid structure?

 

[Philippe]

Yes exactly, I noticed that I can obtain the fourth equation from the first three so I need a fourth independent one.
But I'm under the impression that it is a single structure, I guess I'm wrong!

 

[haruspex]

Yes exactly, I noticed that I can obtain the fourth equation from the first three so I need a fourth independent one.
But I'm under the impression that it is a single structure, I guess I'm wrong!

Imagine replacing one of the end supports with a roller. Can you visualise what would happen in reality?

 

[Philippe]

The horizontal component of the reaction force would be zero as it free to move in this direction on the end support, right?

 

[haruspex]

The horizontal component of the reaction force would be zero as it free to move in this direction on the end support, right?

Yes, but what would happen to the structure? Would it stay up?

 

[Philippe]

No, it would collapse.

 

[haruspex]

No, it would collapse.

How, exactly?

 

[Philippe]

The whole structure would "flatten" and be pushed to the right?

 

[haruspex]

The whole structure would "flatten" and be pushed to the right?

To change shape, some joint must flex. Which one?

 

[Philippe]

Joint e ?

 

[haruspex]

Joint e ?

Right. So the truss system is not in itself a rigid body. Rather, it is two rigid bodies hinged at e. This allows you to write a torque balance equation which is independent of the equations you already have.
Can you see how to do that?

 

[Philippe]

Yes it worked!
Thanks a million!