Stationary points classification using definiteness of the Lagrangian

[fatpotato]

Homework Statement

Find the max/min/saddle points of $f(x,y) = x^4 - y^4$ subject to the constraint $g(x,y) = x^2-2y^2 -1 =0$
Use Lagrange multipliers method
Classify the stationnary points (max/min/saddle) using the definiteness of the Hessian

Relevant Equations

Positive/Negative definite matrix

Hello,

I am using the Lagrange multipliers method to find the extremums of $f(x,y)$ subjected to the constraint $g(x,y)$, an ellipse.

So far, I have successfully identified several triplets $(x^∗,y^∗,λ^∗)$ such that each triplet is a stationary point for the Lagrangian: $\nabla \mathscr{L} (x^∗,y^∗,λ^∗) = 0$

Now, I want to classify my triplets as max/min/saddle points, using the positive/negative definiteness of the Hessian like I have been doing for unconstrained optimization, so I compute what I think is the Hessian of the Lagrangian:

$$H_{\mathscr{L}}(x,y,λ)= \begin{pmatrix} 12x^2 - 2\lambda & 0 \\ 0 & -12y^2 - 4\lambda \end{pmatrix}$$

Evaluating the Hessian for my first triplet $(0,\pm \frac{\sqrt{2}}{2},−\frac{1}{2})$ gives me:

$$H_{\mathscr{L}}(0,\pm \frac{\sqrt{2}}{2},−\frac{1}{2}) = \begin{pmatrix} 1 & 0 \\ 0 & - 4\end{pmatrix}$$

This matrix is diagonal, meaning that we immediately read its eigenvalues on the diagonal: $\lambda_1 = 1 > 0$ and $\lambda_2 = -4 < 0$. A positive/negative definite matrix has only positive/negative eigenvalues, thus I conclude that this matrix is neither, due to its eigenvalues' opposite signs.

When I was studying unconstrained optimization, I learned that we have in this case a saddle point, so I would like to think that the points $(0,\pm \frac{\sqrt{2}}{2})$ are both saddle points for my function f, however, the solution to this problem affirms these points are minimums, using the following argument:

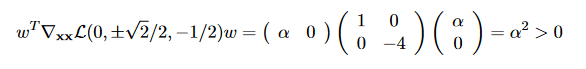
Using the fact that $\nabla g(x,y) = (0,\pm \frac{\sqrt{2}}{2})$ and that $w^T \nabla g(x,y) = 0$ if and only if $w = (\alpha, 0), \alpha \in \mathbb{R}^{\ast}$

I thought that it was enough to check for the definiteness of the Hessian, and now I am really confused...

Here are my questions:

1. When is it enough to check the definiteness of the Hessian to classify stationnary points?
2. Why is there this additional step in constrained optimization?
3. What am I missing?

Thank you for your time.

Edit: PF destroyed my LaTeX formatting.

 

[pasmith]

You are constrained to look at the behaviour of $f$ restricted to the one-dimensional hyperbola $g(x,y) = x^2 - 2y^2 - 1 = 0$. If $f$ increases or decreases as you move off this curve, then that does not concern you.

To remain on the curve, your direction of travel must be orthogonal to $\nabla g$. In this case, the eigenvector corresponding to the negative eigenvalue is parallel to $\nabla g$ and the eigenvector corresponding to the positive eigenvalue is orthogonal to it, so as far as you are concerned the negative eigenvalue is irrelevant: this critical point is a minimum.

In general, $\nabla g$ will not be an eigenvector of the hessian of $f$. The text therefore defines a vector $\mathbf{w}$ orthogonal to $\nabla g$) and looks at $$f(\mathbf{x} + \alpha\mathbf{w}) \approx f(\mathbf{x}) + \tfrac12\alpha^2 \mathbf{w}^T H \mathbf{w}$$ to determine whether a critical point of $f$ subject to this constraint is a minimum ($\mathbf{w}^T H\mathbf{w} > 0$) or a maximum ($\mathbf{w}^T H\mathbf{w} < 0$).

 

[fatpotato]

Thank you for your answer. There is a new point I do not understand:

In this case, the eigenvector corresponding to the negative eigenvalue is parallel to and the eigenvector corresponding to the positive eigenvalue is orthogonal to it, so as far as you are concerned the negative eigenvalue is irrelevant: this critical point is a minimum.

How do you deduce that the eigenvector corresponding to the negative eigenvalue is parallel to the gradient? Same question for the eigenvector corresponding to the positive eigenvalue?

 

[pasmith]

Thank you for your answer. There is a new point I do not understand:

How do you deduce that the eigenvector corresponding to the negative eigenvalue is parallel to the gradient? Same question for the eigenvector corresponding to the positive eigenvalue?

By inspection. In this case the Hessian is diagonal, so we immediately see that the eigenvectors are (1,0) with eigenvalue $H_{11} = 1$ and (0,1) with eigenvalue $H_{22} = -4$. $\nabla g$ is easily computed to be $(2x,-4y)$ and at the critical point this is $(0, \pm \sqrt{2})$. The direction orthogonal to it is therefore (1,0).

 

[fatpotato]

Yes of course, we look for the kernel of $H - \lambda_i I$ so the vector $(1,0)^T$ is mapped to $(0,0)^T$ with eigenvalue $\lambda_1 = 1$, thus being the associated eigenvector.

Sorry, I knew the concept, but could not deduce it myself. Now it is perfectly clear, thank you!