jin94
- 4
- 0
Hi! The following image is taken from my note in Stat Mech. Please excuse my ugly handwriting...
I copied this from my professor's note on a whiteboard, and I'm not so sure if it is correct. The equations for Z1 (partition function before mixing) and Z2 (partition function after mixing) seems to imply that Z1 is much larger than Z2 (since N!/(NA! *NB!) is a large number). However, the Z=exp(-bF) then implies that the Helmlholtz free energy before mixing is lower that after mixing, indicating that mixing is not spontaneous. This is against what I have learned so far, since mixing increases entropy and, therefore, spontaneous. Could you please clarify this for me? I have been struggling with this all day long ... thank you so much! If it is hard to read, please let me know.
This is from my note in stat mech.
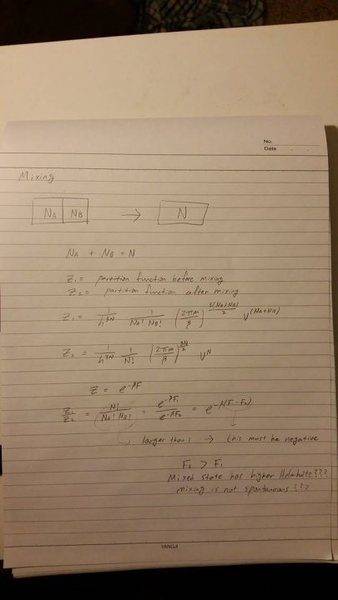
I copied this from my professor's note on a whiteboard, and I'm not so sure if it is correct. The equations for Z1 (partition function before mixing) and Z2 (partition function after mixing) seems to imply that Z1 is much larger than Z2 (since N!/(NA! *NB!) is a large number). However, the Z=exp(-bF) then implies that the Helmlholtz free energy before mixing is lower that after mixing, indicating that mixing is not spontaneous. This is against what I have learned so far, since mixing increases entropy and, therefore, spontaneous. Could you please clarify this for me? I have been struggling with this all day long ... thank you so much! If it is hard to read, please let me know.
This is from my note in stat mech.