- #1
peripatein
- 880
- 0
Hi,
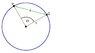
A circle of radius r is as shown in the attached diagram. I am asked to first express X as a function of θ, then to compute E(X). It is also stated that θ obeys U[0,2π].
Through simple trigonometry I have found X = 2rsin(θ/2). As θ distributes evenly, I know that the density of θ should be 1/2π. What is the density of x then? Am I supposed to simply substitute 2arcsin(x/2r)? Or should it be approached by first computing E(θ) and trying to hence infer E(X)?
I'd appreciate an advice.
Homework Statement
A circle of radius r is as shown in the attached diagram. I am asked to first express X as a function of θ, then to compute E(X). It is also stated that θ obeys U[0,2π].
Homework Equations
The Attempt at a Solution
Through simple trigonometry I have found X = 2rsin(θ/2). As θ distributes evenly, I know that the density of θ should be 1/2π. What is the density of x then? Am I supposed to simply substitute 2arcsin(x/2r)? Or should it be approached by first computing E(θ) and trying to hence infer E(X)?
I'd appreciate an advice.