- #1
ak416
- 122
- 0
Ok Whats the general way to solve problems such as these?
-Let X and Y have the joint pdf f_X,Y(x,y) = 2e^-(x+y) , 0 < x < y, 0 < y
Find P(Y < 3X).
-Find P(X < 2Y) if f_X,Y(x,y) = x + y for X and Y defined over the unit interval (meaning from 0 to 1).
I know you have to set up the double integral, like for the first one the answer is:
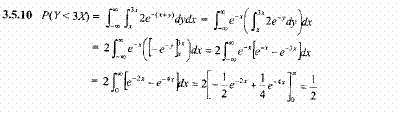
but P(Y < 3X) => P(x > 1/3Y) so why can't you take the integral from 1/3Y to Y wrt X (because x has to be smaller than y) and the integral from 0 to infinity with respect to y (because y has to be greater than 0)?
Note:I am currently taking a multivariable calculus course and I haven't gotten to multi-integration yet, so i would just like to know the general method for determining the boundaries of integration.
I also have other questions (about Transforming random variables) but ill save those for later, I would like to understand this first.
Thanks.
-Let X and Y have the joint pdf f_X,Y(x,y) = 2e^-(x+y) , 0 < x < y, 0 < y
Find P(Y < 3X).
-Find P(X < 2Y) if f_X,Y(x,y) = x + y for X and Y defined over the unit interval (meaning from 0 to 1).
I know you have to set up the double integral, like for the first one the answer is:
but P(Y < 3X) => P(x > 1/3Y) so why can't you take the integral from 1/3Y to Y wrt X (because x has to be smaller than y) and the integral from 0 to infinity with respect to y (because y has to be greater than 0)?
Note:I am currently taking a multivariable calculus course and I haven't gotten to multi-integration yet, so i would just like to know the general method for determining the boundaries of integration.
I also have other questions (about Transforming random variables) but ill save those for later, I would like to understand this first.
Thanks.