Stewart platform and closed loops

[Trying2Learn]

TL;DR Summary

How to compute the orientation

Hello!

(I am not asking for someone to do this for me. I am only asking a qualitative question.)

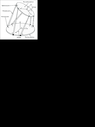
Suppose one knows the lengths of all six links that are involved in the Stewart platform.

Is that enough to define the position and orientation of the top (assuming the base is fixed)

I would take the route of creating six closed loop equations for each of the six struts and using Newton-Raphson (or similar) to
compute pitch, yaw, roll, heave, sway, surge of the top.

However, a colleague is arguing with me that just knowing the lengths of the six arms should be enough.

Picture attached

 

[Filip Larsen]

Have you tried searching for how to solve the Steward platform kinematics?

 

[Trying2Learn]

Have you tried searching for how to solve the Steward platform kinematics?

No, but that is because I know how I would do it: write six closed loop equations.

I am more interested in why my colleague insists that just knowing the lengths, is sufficient.
(Actually I did do a search, but most is about the dynamics of it, and I am not focused on that.)

I really want to understand if just knowing the lengths (and some fundamental geometry) is sufficient.
For I would solve the non linear closed loop equations using Newton Raphson (or something like that).

In other words: assume a pitch yaw roll heave sway surge of the top plate. Then, travel from the bottom center, up to the midpoint ( unknowns for position), and then out and back down (involving the pitch, yaw and roll). Get the six non-linear equations and solve.

My colleauge insists that is too complicated and that simple geometry and the six lengths are enough. I don't think so.

 

[Trying2Learn]

Have you tried searching for how to solve the Steward platform kinematics?

In other words...

If i take off the top plate and remove the six struts, I have six struts of known length.

Now I have to reassemble the platform, but all I have are six legs of specific length -- and I do not think I can reassemble it: he insists it is possible. I think there is too much uncertainty about the orientation of the legs.

I think that that it is NOT geometrically simple (like my colleagues says) and does require a non-linear analysis.

 

[Filip Larsen]

To me it still sounds like you are asking if the (forward) kinematic problem can be solved in closed form, a question which I believed can be answered by searching for how to solve that problem. That the problem is described as a problem in kinematic does not mean it is only relevant for when the platform is moving.

Alternatively you can perhaps enter into a dialog with your colleagues to settle the details. In any case it is hard for us to guess what you or your colleagues mean during some discussion you had.