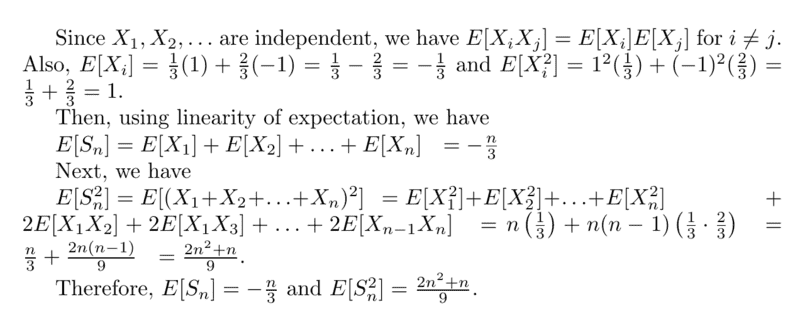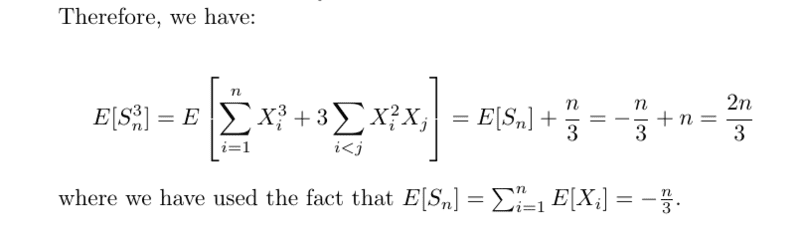SUMMARY
The discussion focuses on the calculation of expected values for independent random variables in stochastic calculus, specifically for the expressions E(S_n), E(S_n^2), and E(S_n^3). The correct expressions are identified as E(S_n) = -n/3, E(S_n^2) = n + n(n-1)/9, and E(S_n^3) = -n/3 - n(n-1)/2 - n(n-1)/9. Participants emphasize the importance of using multinomial coefficients when expanding expressions and correcting careless mistakes in calculations.
PREREQUISITES
- Understanding of stochastic calculus concepts, particularly conditional expectation.
- Familiarity with independent random variables and their properties.
- Knowledge of multinomial coefficients and their application in probability.
- Ability to perform algebraic manipulations involving expected values.
NEXT STEPS
- Study the application of multinomial coefficients in probability theory.
- Learn how to derive expected values for sums of independent random variables.
- Explore advanced topics in stochastic processes, focusing on conditional expectations.
- Practice solving problems involving the calculation of E(S_n) for various distributions.
USEFUL FOR
Students and professionals in mathematics, statistics, and finance who are working with stochastic processes and need to understand the intricacies of conditional expectation and expected value calculations.