bigfish2000
- 4
- 0
I need a formula for deriving the required material thickness for an acrylic panel.
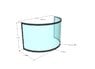
The project will involve an acrylic window for a large aquarium. I have included a dimensional rendering.
The maximum design stress must be maintained at or below 800PSI.
The maximum water pressure inside the aquarium will be 2.6662 PSI above atmospheric.
The panel will be used in a vertical position as detailed in the rendering.
The load force (wet) will be on the concave side.
The panel will have concrete support along all four edges as outlined in gray. The viewing portion is shown translucent in the rendering.
The mechanical properties of acrylic are as follows.
Tensile strength: 10,000 PSI
Elongation, Rupture: 4.2%
Modulus of Elasticity: 400,000 PSI
Flexural Strength: 16,500 PSI
Modulus of Elasticity: 475,000 PSI
Compressive Strength: 18,000 PSI
Modulus of Elasticity: 430,000 PSI
Shear Strength: 9,000 PSI
Impact Strength .4ft lbs/in
Rockwell hardness: M-94
If you need any additional information please let me know.
Thank you for the assistance.
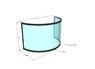
The project will involve an acrylic window for a large aquarium. I have included a dimensional rendering.
The maximum design stress must be maintained at or below 800PSI.
The maximum water pressure inside the aquarium will be 2.6662 PSI above atmospheric.
The panel will be used in a vertical position as detailed in the rendering.
The load force (wet) will be on the concave side.
The panel will have concrete support along all four edges as outlined in gray. The viewing portion is shown translucent in the rendering.
The mechanical properties of acrylic are as follows.
Tensile strength: 10,000 PSI
Elongation, Rupture: 4.2%
Modulus of Elasticity: 400,000 PSI
Flexural Strength: 16,500 PSI
Modulus of Elasticity: 475,000 PSI
Compressive Strength: 18,000 PSI
Modulus of Elasticity: 430,000 PSI
Shear Strength: 9,000 PSI
Impact Strength .4ft lbs/in
Rockwell hardness: M-94
If you need any additional information please let me know.
Thank you for the assistance.