Why Does Integration Matter in Solving for the Average Value of a Function?

  • Context: MHB 
  • Thread starter Thread starter nghijen
  • Start date Start date
Click For Summary
SUMMARY

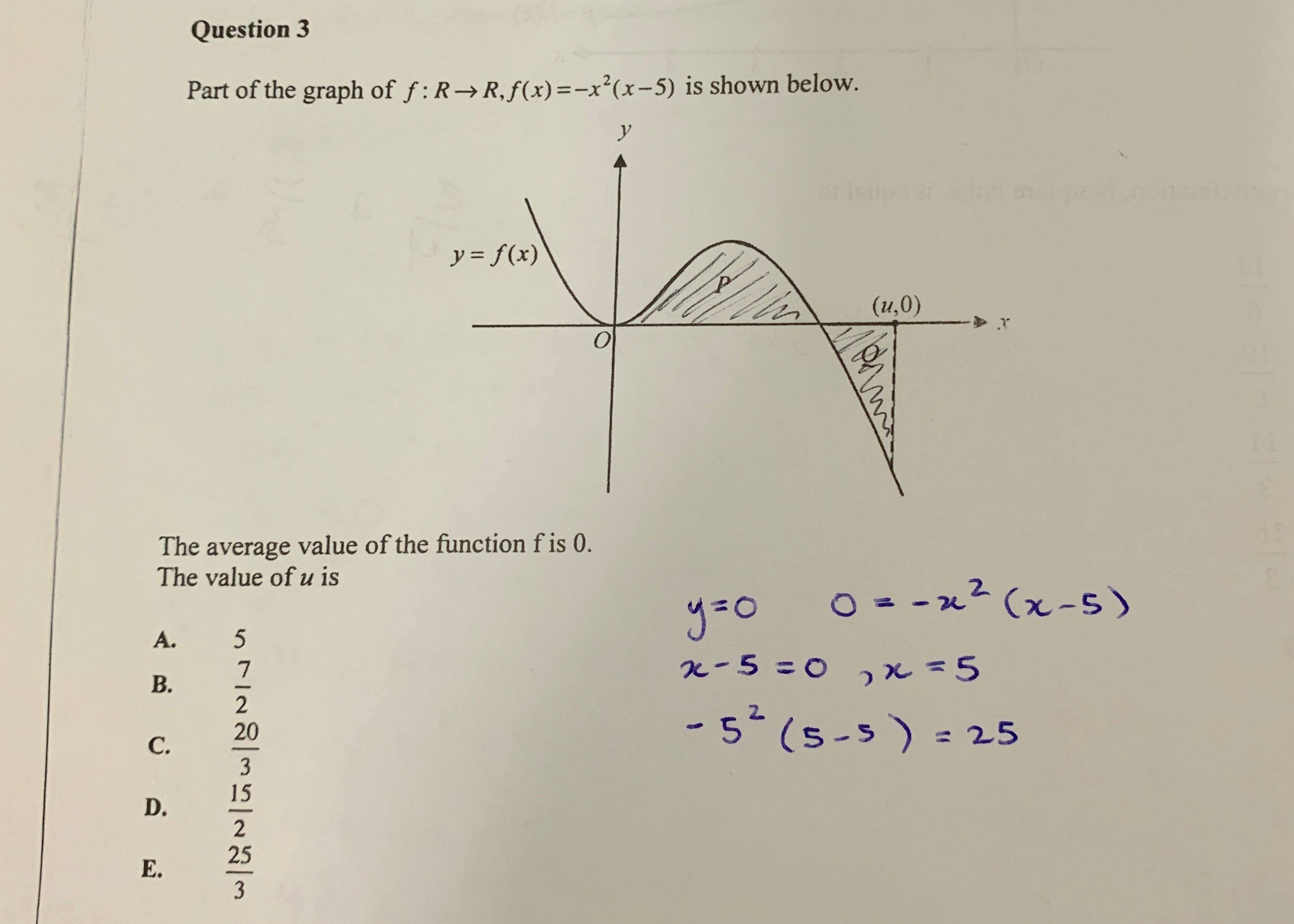
The discussion centers on the calculation of the average value of a function using definite integrals, specifically the function \( f(x) = x^2(5-x) \) over the interval \([0, u]\). The average value is defined as \(\frac{1}{u-0} \int_0^u f(x) \, dx\). Participants highlight the importance of correctly identifying the interval and performing the integration, noting that the average value formula requires proper execution of the integral. Miscalculations, such as incorrectly evaluating \( -5^2(5-5) \), lead to confusion regarding the function's roots.

PREREQUISITES
  • Understanding of definite integrals in calculus
  • Familiarity with the concept of average value of a function
  • Knowledge of polynomial functions and their properties
  • Ability to perform integration techniques
NEXT STEPS
  • Study the properties of definite integrals in calculus
  • Learn how to calculate the average value of a function using integration
  • Explore polynomial function behavior and roots
  • Practice integration techniques with various functions
USEFUL FOR

Students learning calculus, educators teaching integration concepts, and anyone seeking to understand the average value of functions through definite integrals.

nghijen
Messages
2
Reaction score
0
I have attempted to solve the question but I still do not understand. Can someone please help me?
IMG_5255.jpeg
 
Physics news on Phys.org
average value of a function involves a definite integral over an interval ... from your shading, is the given interval $[0,u]$ ?
 
skeeter said:
average value of a function involves a definite integral over an interval ... from your shading, is the given interval $[0,u]$ ?

I am assuming it is [0, u] !
 
nghijen said:
I am assuming it is [0, u] !

$\displaystyle 0 = \dfrac{1}{u-0} \int_0^u x^2(5-x) \, dx$

work it ...
 
I frankly can't understand what you think you are doing! Much of what you are doing is determining where f(x)= 0. Okay that is at x= 5, which you have, and x= 0, which you ignore, but that is irrelevant anyway! The average value of a function, f(x), over interval a to b is the integral of f, from a to b, divided by b- a. But you show no attempt at integration!

Oh, and $-5^2(5- 5)= 0$, not -25! That is why you got x= 5 as a solution to $-x^2(x- 5)= 0$!
 
Last edited:

Similar threads

MHB Using advanced calculus for finding values
  • · Replies 2 ·
Replies
2
Views
1K
High School Some questions while I self-learn Applied Calculus
  • · Replies 49 ·
2
Replies
49
Views
7K
High School Does U-Substitution Function as the Inverse of the Chain Rule?
  • · Replies 10 ·
Replies
10
Views
2K
High School Explain Integration to me, please
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Infinite Series - Divergence of 1/n question
  • · Replies 5 ·
Replies
5
Views
2K
MHB Indefinite integral in division form
  • · Replies 1 ·
Replies
1
Views
2K
High School Why don't we account for the constant in integration by parts?
  • · Replies 16 ·
Replies
16
Views
4K
Undergrad Integration with different infinitesimal intervals
  • · Replies 31 ·
2
Replies
31
Views
4K
Undergrad Why is the integral of ##\arcsin(\sin(x))## so divisive?
  • · Replies 3 ·
Replies
3
Views
3K
Undergrad Should the function f to be continuous for applying MVTI or not?
  • · Replies 4 ·
Replies
4
Views
1K