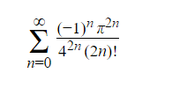SUMMARY
The discussion centers on finding the sum of the infinite series that equals 1/sqrt(2). The user initially attempted the ratio test but found it unhelpful. A key insight provided is that the series in question is the power series expansion for cos(π/4), specifically represented as ∑_{n=0}^∞ (-1)^n/(2n)! (π/4)^{2n}. This aligns with the standard power series for cos(x), confirming the result of 1/sqrt(2>.
PREREQUISITES
- Understanding of infinite series and convergence tests
- Familiarity with power series expansions
- Knowledge of trigonometric functions and their series representations
- Proficiency in mathematical notation and summation conventions
NEXT STEPS
- Study the ratio test for convergence of series in detail
- Explore power series expansions for other trigonometric functions
- Learn about Taylor series and their applications
- Investigate the relationship between trigonometric functions and their limits
USEFUL FOR
Students and educators in mathematics, particularly those focused on calculus and series analysis, as well as anyone seeking to deepen their understanding of infinite series and trigonometric functions.