DivergentSpectrum
- 149
- 15
we say the surface element of x(u,v),y(u,v),z(u,v) is absolute value of the cross product
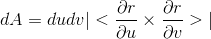
or
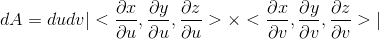
i don't understand why this is. i know that the absolute value of the cross product
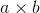 is the area of a parallelogram formed by a,b,a+b, but i get lost after that
is the area of a parallelogram formed by a,b,a+b, but i get lost after that
im guessing something happens where dudv cancels out with ∂u∂v then just leaves ∂r, but i can't really figure what it means.
anyone whos got into computer graphics can tell you triangles are the building blocks of surfaces, because any 3 points occupy the same plane. why a parallelogram then?
or
i don't understand why this is. i know that the absolute value of the cross product
im guessing something happens where dudv cancels out with ∂u∂v then just leaves ∂r, but i can't really figure what it means.
anyone whos got into computer graphics can tell you triangles are the building blocks of surfaces, because any 3 points occupy the same plane. why a parallelogram then?
Last edited: