GONURVIA said:
Hi all, this is my first thread!
I am having problems trying to find the way of drawing a line which is tangent to a circle and intersects another circle making a 30º intersection.
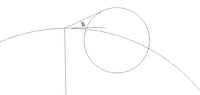
Let´s say I have circle A with coordinates 479183.87, 4365099.87 (x1,y1) and a radius of 27780m. I have a second circle, B, with coordinates 488889.66, 4390316.69 (x2,y2) and a radius of 5294m. I would like to draw a line which joins both circle, being the line tangent to circle B and intersects circle A with 30º to its circumference. I've attached an image hoping it helps visually to figure out what I'm trying to ask for
I hope I explained myself correctly. Thanks everyone!
Hi GONURVIA, and welcome to MHB!
[TIKZ][scale=6]
\clip (7,8.25) rectangle (10,9.6) ;
\draw (7.92,6.51) circle (2.78cm) ;
\draw (8.89,9.03) circle (0.53cm) ;
\coordinate [label=above:$C$] (C) at (8.16,9.28) ;
\coordinate [label=above:$D$] (D) at (8.666,9.512) ;
\draw (9.156,9.193) -- (C) -- (D) ;
\draw (7.92,6.51) -- (C) ;
[/TIKZ]
I assume that $(x_1,y_1)$ and $(x_2,y_2)$ are the centres of the two circles.
Let $C$ be the point where the tangent line meets circle $A$. Suppose that the radius there (the line from $(x_1,y_1)$ to $C$) makes an angle $\theta$ with the horizontal axis. Denoting the radius of circle $A$ by $R$, the coordinates of $C$ are $(x_1+R\cos\theta,y_1+R\sin\theta)$. The tangent to circle $B$ then has to be at an angle $\theta-60^\circ$ to the horizontal. So the equation of the tangent line is $$y-y_1-R\sin\theta = \tan(\theta-60^\circ)(x-x_1-R\cos\theta).$$ Using a bit of trigonometry, that becomes $$(x-x_1)\sin(\theta-60^\circ) - (y-y_1)\cos(\theta-60^\circ) + R\sin(60^\circ) = 0.$$ The condition for that line to be a tangent to circle $B$ is that the distance from $(x_2,y_2)$ to the line should be equal to $r$, the radius of circle $B$. The formula for the distance from a point to a line then gives the equation $$(x_2-x_1)\sin(\theta-60^\circ) - (y_2-y_1)\cos(\theta-60^\circ) + R\sin(60^\circ) = r.$$ (Strictly speaking, the left side of that equation should have absolute value signs round it. But since it turns out that it is already positive, I have left them out.)
Let $\alpha$ be the angle such that $\tan\alpha = \dfrac{y_2-y_1}{x_2-x_1}.$ Then a further bit of trigonometry shows that $$\sin(\theta-\alpha - 60^\circ) = \frac{r-R\sin(60^\circ)}{\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}}.$$ You can then start putting in the numerical values for $x_1,x_2,y_1,y_2,R$ and $r$, to find first $\alpha$, then $\theta$ and then the coordinates for $C$.
I only have a small pocket calculator, so I can only work to a few significant figures. The results I get are $$\alpha \approx 68.95^\circ,$$ $$\theta \approx 84.97^\circ,$$ $$C \approx (481600,4392800).$$ Finally, the point $D$ where the tangent line touches circle $B$ is given by $D = (x_2 + r\cos(\theta+30^\circ), y_2+r\sin(\theta+30^\circ))$, or approximately $(486600,4395100)$.