Tangential and Radial Acceleration of car around a curve

[123scope]

Hi, I have a problem with this problem..
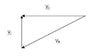
The figure (in the attachment) shows a bird's-eye view of a car going around a highway curve. As the car moves from point 1 to point 2, its speed doubles. Which vector shows the direction of the car's average acceleration between these two points?

Ok. According to my knowledge,
THe answer cannot be (g) and (b) and (a) is also unlikely
Applying the radial and tangential acceleration I guess it could be (d) and (f)
But I can't make my mind... Can anyine help me.

 

[Andrew Mason]

Start with the definition of average acceleration: \Delta{\vec{v}}/\Delta t.

Draw the initial velocity vector. Draw the final velocity vector. The change in velocity is the difference between those two vectors. That should enable you to choose the correct answer.

AM

 

[123scope]

So using a = (vf - vi) / (delta t)

I get a = (-2v i - v j) / (delta t)

So does that mean the direction of the average acceleration is in the third quadrant??

 

[Andrew Mason]

So using a = (vf - vi) / (delta t)

I get a = (-2v i - v j) / (delta t)

So does that mean the direction of the average acceleration is in the third quadrant??

Don't bother putting them on an cartesian plane - just use North/South etc. The initial velocity vector is 1 unit North and the final velocity is 2 units west. Where does the difference vector point?

AM

 

[123scope]

The vector diagram is as follows/
I found it to be south west. So could it be option (g)?

 

[Andrew Mason]

The vector diagram is as follows/
I found it to be south west. So could it be option (g)?

What is the angle (south of west) that the resultant points in your diagram? What is the angle in g)? (You can measure the latter if you can't tell just by looking at it).

AM

 

[123scope]

sorry woops. it the answer can't be option (g). THe angle in option (g) is slightly larger.
The answer should be (f) then.
26.57 degrees south of west. Am I right?

 

[Andrew Mason]

sorry woops. it the answer can't be option (g). THe angle in option (g) is slightly larger.
The answer should be (f) then.
26.57 degrees south of west. Am I right?

Right.

AM