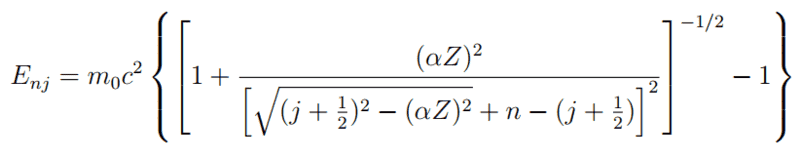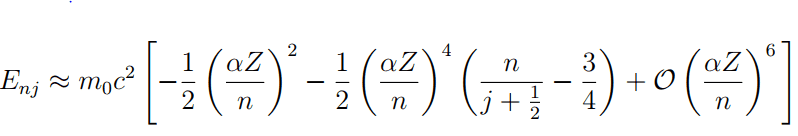SUMMARY
The forum discussion focuses on performing a Taylor expansion of the energy levels derived from Dirac's equation under a Coulomb potential, specifically in orders of (αZ/n)². Participants emphasize the importance of simplifying the expression by first expanding the term √((j+1/2)² - (αZ)²) as a Taylor series, which significantly reduces complexity. Key insights include retaining the second-order term of the (αZ/n)² factor to achieve accurate results, as well as correcting earlier miscalculations that led to discrepancies in the fourth-order term. Ultimately, the correct approach yields a final result consistent with established values.
PREREQUISITES
- Understanding of Dirac's equation and its implications in quantum mechanics.
- Familiarity with Taylor series expansions and their applications in physics.
- Knowledge of Coulomb potential and its role in quantum systems.
- Proficiency in mathematical manipulation of series and derivatives.
NEXT STEPS
- Study the derivation of energy levels in quantum mechanics using Dirac's equation.
- Learn advanced techniques for Taylor series expansions in quantum physics contexts.
- Explore the implications of Coulomb potential in atomic and subatomic systems.
- Investigate the significance of higher-order terms in perturbation theory.
USEFUL FOR
Physicists, particularly those specializing in quantum mechanics, theoretical physicists working with relativistic equations, and students seeking to deepen their understanding of energy levels in quantum systems influenced by Coulomb potentials.