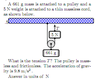
SUMMARY
The discussion focuses on calculating the tension T in a massless, frictionless pulley system with two weights: m1 at 661 g and w2 at 5 N. The correct approach involves using free-body diagrams to analyze the forces acting on each mass. The user initially miscalculated tension by incorrectly assuming T equals the sum of weights. It is established that the tension in each segment of the rope may differ, necessitating a detailed examination of the system's dynamics.
PREREQUISITES
- Understanding of Newton's laws of motion
- Knowledge of free-body diagrams
- Basic principles of tension in pulley systems
- Ability to convert units (grams to kilograms)
NEXT STEPS
- Study the principles of tension in non-equilibrium systems
- Learn to draw and analyze free-body diagrams for complex systems
- Explore the effects of mass and weight on tension in pulley systems
- Review examples of massless and frictionless pulley problems in physics textbooks
USEFUL FOR
Students studying physics, particularly those focusing on mechanics and pulley systems, as well as educators seeking to clarify concepts related to tension and free-body diagrams.