SUMMARY
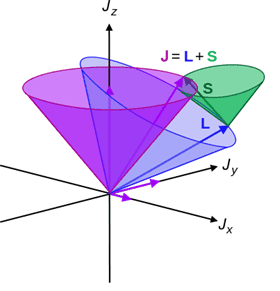
The average value of the S operator in quantum mechanics, specifically in the context of spin-orbit coupling as discussed in David Griffith's "Introduction to Quantum Mechanics," is the projection of S onto J. The fine-structure Hamiltonian is defined as H = A∇L · ∇S. The commutator [H, ∇S] results in iA∇S × ∇L, which can be expressed as iA∇S × ∇J due to the relationship ∇J = ∇L + ∇S. Applying the Ehrenfest theorem leads to the time evolution equation for the average value of S, indicating that only the perpendicular component of S exhibits time dependence, akin to the precession of a spinning top.
PREREQUISITES
- Understanding of quantum mechanics principles, particularly spin and angular momentum.
- Familiarity with the Ehrenfest theorem and its application in quantum mechanics.
- Knowledge of vector algebra and cross products in the context of quantum operators.
- Basic comprehension of Hamiltonians in quantum systems, specifically fine-structure Hamiltonians.
NEXT STEPS
- Study the Ehrenfest theorem in detail to understand its implications in quantum mechanics.
- Learn about the mathematical formulation of angular momentum operators in quantum mechanics.
- Explore the concept of spin-orbit coupling and its significance in atomic physics.
- Investigate the dynamics of precession in quantum systems and its relation to classical mechanics.
USEFUL FOR
Students and researchers in quantum mechanics, physicists studying atomic structure, and anyone interested in the mathematical foundations of spin dynamics and precession in quantum systems.