Spin-Orbit Coupling in Hydrogen Atom: Understanding the Calculation

[Viona]

Homework Statement

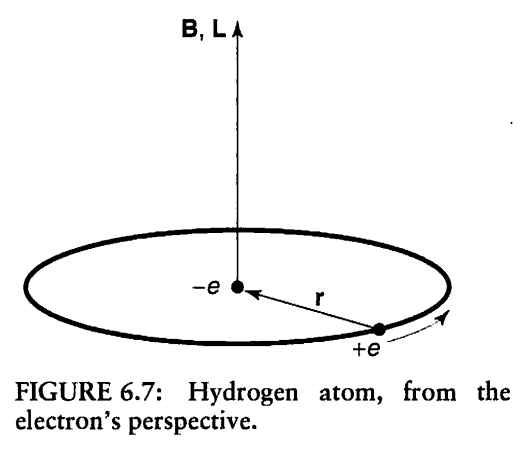
Why we calculate the magnetic field of the proton (B) using the angular momentum of the electron (L)?

Relevant Equations

Why we had to do this calculations in the rest frame
of the electron?

I was reading in the Book: Introduction to Quantum Mechanics by David J. Griffiths. In chapter Time-independent Perturbation Theory, Section: Spin -Orbit Coupling. I understood that the spin–orbit coupling in Hydrogen atom arises from the interaction between the electron’s spin magnetic moment, and the proton’s orbital magnetic field B. But I did not understand why He calculated the magnetic field of the proton (B) using the angular momentum of the electron (L)! Please see the attached pictures. Thank you!

 

[kuruman]

You can answer your question by looking at the derivation. The expression $B=\dfrac{\mu_0I}{2r}$ gives the B-field at the center of a loop of radius $r$. That is why one starts in the reference frame of the electron. The question then is, what do we do with the current $I$ which is not a quantum mechanical operator? The answer to that is, cast the current in terms of the angular momentum of the electron which is a quantum mechanical operator. One can use the angular momentum of the electron $L=m_evr$ because the period $T$ of the electron around the proton is the same as the period of the proton around the electron.

 

[Viona]

You can answer your question by looking at the derivation. The expression $B=\dfrac{\mu_0I}{2r}$ gives the B-field at the center of a loop of radius $r$. That is why one starts in the reference frame of the electron. The question then is, what do we do with the current $I$ which is not a quantum mechanical operator? The answer to that is, cast the current in terms of the angular momentum of the electron which is a quantum mechanical operator. One can use the angular momentum of the electron $L=m_evr$ because the period $T$ of the electron around the proton is the same as the period of the proton around the electron.

I though the periodic time and the radius of the rotation are affected by the relativistic motion, so the periodic time from the point view of the electron will be different from the point view of the proton.

 

[DrClaude]

I though the periodic time and the radius of the rotation are affected by the relativistic motion, so the periodic time from the point view of the electron will be different from the point view of the proton.

This is non-relativistic quantum mechanics.

 

[Viona]

You can answer your question by looking at the derivation. The expression $B=\dfrac{\mu_0I}{2r}$ gives the B-field at the center of a loop of radius $r$. That is why one starts in the reference frame of the electron. The question then is, what do we do with the current $I$ which is not a quantum mechanical operator? The answer to that is, cast the current in terms of the angular momentum of the electron which is a quantum mechanical operator. One can use the angular momentum of the electron $L=m_evr$ because the period $T$ of the electron around the proton is the same as the period of the proton around the electron.

Yes the period the same. But The direction of the angular momentum is parallel to the direction of the magnetic field, then the electron orbital momentum vector should point to the opposite direction?

 

[DrClaude]

then the electron orbital momentum vector should point to the opposite direction?

Why would it point in the opposite direction?

 

[Viona]

Why would it point in the opposite direction?

Sorry, the electron's orbital momentum points in the same direction of the magnetic field. Thanks!