greswd
- 764
- 20
You might have seen such a 3-D map of the stars before:
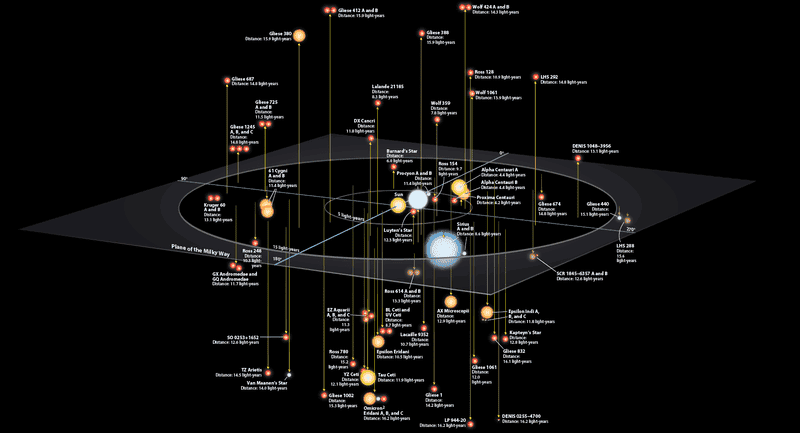 And I was wondering about a 3-D map if space was non-Euclidean, what would be the best ways to display it.
And I was wondering about a 3-D map if space was non-Euclidean, what would be the best ways to display it.
To keep it simple, if you're considering elliptic space, you can consider the entire "global" map. Just like we have world maps of our entire ellipsoidal globe of planet Earth.
And if you're considering hyperbolic space, you can also consider a closed seamless hyperbolic universe in addition to an "open" hyperbolic space.
Another factor to consider is whether the map is static or interactive. Though the region of space which we'll be displaying will be so large that the non-Euclidean geometry will be obvious, it won't be like zooming into a tiny portion of space which appears relatively "flat" and Euclidean.
To keep it simple, if you're considering elliptic space, you can consider the entire "global" map. Just like we have world maps of our entire ellipsoidal globe of planet Earth.
And if you're considering hyperbolic space, you can also consider a closed seamless hyperbolic universe in addition to an "open" hyperbolic space.
Another factor to consider is whether the map is static or interactive. Though the region of space which we'll be displaying will be so large that the non-Euclidean geometry will be obvious, it won't be like zooming into a tiny portion of space which appears relatively "flat" and Euclidean.