The biomechanics of elbow extension

[thegoose]

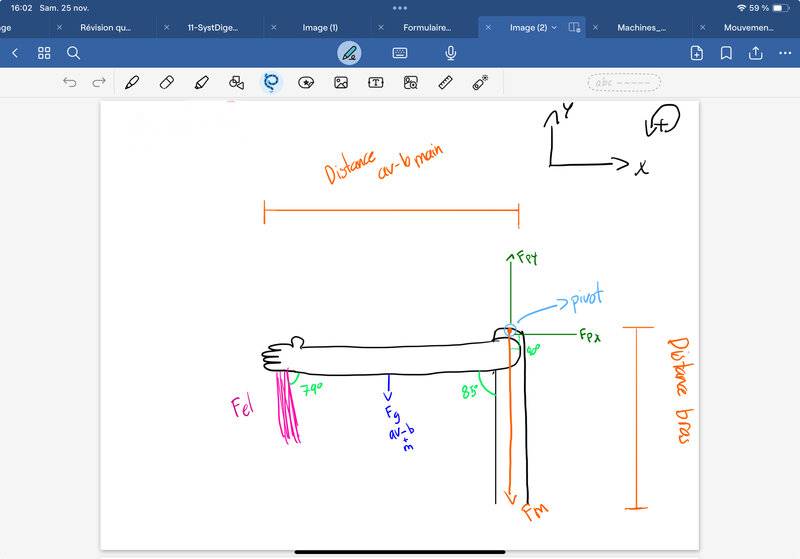
Homework Statement

I noticed that when I do a calculation of the form 85-90 it gives a result of -5, which affects my overall answer by giving a negative number. I think I didn't correctly determine the angle of my muscle strength. Would it be possible for this angle to be 0°? So, by doing the 85-0 calculation, we would get a positive number.

Relevant Equations

Σ𝐹⃗ = 0

X=

Σ𝐹𝑥 = 0

−𝐹𝑃𝑥 + 𝐹𝑀 sin (𝛽 − 90°) + 𝐹𝑒𝑙 sin (180 − 𝛽 − 𝜃) = 0

𝐹𝑃𝑥 = 𝐹𝑀 sin ( 𝛽 − 90°) +𝐹𝑒𝑙 sin(180 − 𝛽 − 𝜃)

𝐹𝑃𝑥 = 93.6650N sin (85 − 90) + 28.11N sin(180 − 85 − 79)

Fpx= -8.16344N +7.74816N

𝐹𝑃𝑥 = -0.4154 N←

 

[haruspex]

Please define all your variables.
I assume FM means the force exerted by a muscle, but it seems to be exerted directly down at the shoulder pivot, which is not going to achieve anything. You need to analyse torques, not just forces, and consider the shoulder joint in more detail.