Petrus
- 702
- 0
Exempel 6: If $$g(s, t) = f(s^2-t^2, t^2-s^2)$$ and f is differentiable, show that g satisfies the equation
$$t\frac{dg}{ds}+s\frac{dg}{dt}=0$$
I always try solve it before I look 'soloution' so this is how we both did it. (remember this is a exempel in my book so they show how to solve it but they did not make any tree driagram etc.)
$$\frac{dg}{ds}=\frac{df}{dx}\frac{dx}{ds}+\frac{df}{dy}\frac{dy}{ds}=\frac{df}{dx}(2s)+\frac{df}{dy}(-2s)$$
$$\frac{dg}{dt}=\frac{df}{dx}\frac{dx}{dt}+\frac{df}{dy}\frac{dy}{dt}=\frac{df}{dx}(-2t)+\frac{df}{dy}(2t)$$
$$t\frac{dg}{ds}+s\frac{dg}{dt}=\frac{df}{dx}(2st)+ \frac{df}{dy}(-2st) - \frac{df}{dx}(2st)+\frac{df}{dy}(2st)=0$$
This is what I made extra cause I want to be specefic. I want to citat from my book:
"We got n variables ($$x_1,x_2,...x_n$$ (in this problem we got 2) and each of these $$x_j$$ is a differentiable function of the m vavariables $$t_1, t_2,...,t_m$$ then u is a function of $$t_1,t_2,...,t_m$$ (in our it will be 2 if I understand correct but I strugle on that one)"
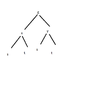
So now I did write about these note and got same answer as the soloution. Then I wanted to draw a 'tree driagram' and I did draw it like this, correct me if I do it wrong View attachment 735
Regards,
$$t\frac{dg}{ds}+s\frac{dg}{dt}=0$$
I always try solve it before I look 'soloution' so this is how we both did it. (remember this is a exempel in my book so they show how to solve it but they did not make any tree driagram etc.)
$$\frac{dg}{ds}=\frac{df}{dx}\frac{dx}{ds}+\frac{df}{dy}\frac{dy}{ds}=\frac{df}{dx}(2s)+\frac{df}{dy}(-2s)$$
$$\frac{dg}{dt}=\frac{df}{dx}\frac{dx}{dt}+\frac{df}{dy}\frac{dy}{dt}=\frac{df}{dx}(-2t)+\frac{df}{dy}(2t)$$
$$t\frac{dg}{ds}+s\frac{dg}{dt}=\frac{df}{dx}(2st)+ \frac{df}{dy}(-2st) - \frac{df}{dx}(2st)+\frac{df}{dy}(2st)=0$$
This is what I made extra cause I want to be specefic. I want to citat from my book:
"We got n variables ($$x_1,x_2,...x_n$$ (in this problem we got 2) and each of these $$x_j$$ is a differentiable function of the m vavariables $$t_1, t_2,...,t_m$$ then u is a function of $$t_1,t_2,...,t_m$$ (in our it will be 2 if I understand correct but I strugle on that one)"
So now I did write about these note and got same answer as the soloution. Then I wanted to draw a 'tree driagram' and I did draw it like this, correct me if I do it wrong View attachment 735
Regards,