ddddd28
- 73
- 4
Hello,
Consider the next scenario:
I wish to travel from point a to point b as fast as possible. Between the points there is a border. In the region from a to the border, I can move only with velocity v1, and after the border, I am allowed to move only with velocity v2. All the additional details are given in the sketch:
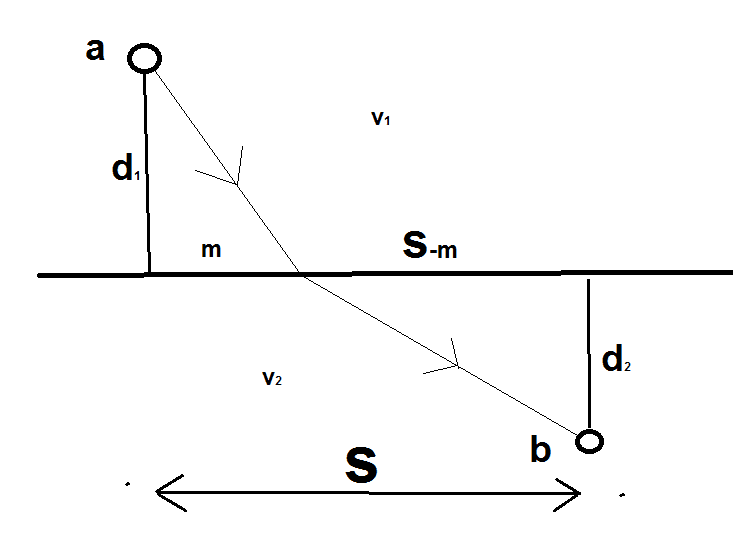
As it turns out, the problem is not as easy as it appears to be because it is not clear where I should pass the border. If v1 is bigger than v2 then I should consider taking a longer route in the first section to compensate on the time spent in the second section. However, a longer route in the first section adds up to the overall distance.
My attempt to solve it was to express the overall duration of the route as a function of m and minimize it. To my dismay, I ended up with a fourth-degree equation that didn't want to crack...
Consider the next scenario:
I wish to travel from point a to point b as fast as possible. Between the points there is a border. In the region from a to the border, I can move only with velocity v1, and after the border, I am allowed to move only with velocity v2. All the additional details are given in the sketch:
As it turns out, the problem is not as easy as it appears to be because it is not clear where I should pass the border. If v1 is bigger than v2 then I should consider taking a longer route in the first section to compensate on the time spent in the second section. However, a longer route in the first section adds up to the overall distance.
My attempt to solve it was to express the overall duration of the route as a function of m and minimize it. To my dismay, I ended up with a fourth-degree equation that didn't want to crack...