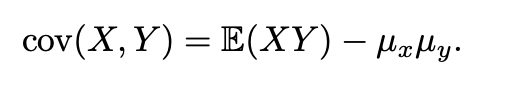The joint probability - two coins

[docnet]

Homework Statement

.

Relevant Equations

.

(a)

The probability mass function of X and Y:

$$p_{X,Y}(1,1)= \frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$$
$$p_{X,Y}(1,0)=\frac{1}{2}\cdot \frac{1}{4}=\frac{1}{8}$$
$$p_{X,Y}(0,1)= \frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$$
$$p_{X,Y}(0,0)= \frac{1}{2}\cdot \frac{1}{4}=\frac{1}{8}$$

or

$$
p_{X,Y}(a,b)=
\begin{cases}
\frac{3}{8} & (a,b)=(1,1) \quad \text{or}\quad(a,b)=(0,1) \\
\frac{1}{8} & (a,b)=(1,0) \quad \text{or}\quad(a,b)=(0,0)
\end{cases}$$

(b)

The marginal distribution of X is

$$p_X(1)=p_{X,Y}(1,0)+p_{X,Y}(1,1)=\frac{1}{2}\frac{3}{4}+\frac{1}{2}\frac{1}{4}=\frac{1}{2}$$
$$p_X(0)=p_{X,Y}(0,0)+p_{X,Y}(0,1)=\frac{1}{2}\frac{1}{4}+\frac{1}{2}\frac{3}{4}=\frac{1}{2}$$

The marginal distribution of Y is

$$p_Y(1)=p_{X,Y}(0,1)+p_{X,Y}(1,1)=\frac{1}{2}\frac{3}{4}+\frac{1}{2}\frac{1}{4}=\frac{3}{4}$$
$$p_Y(0)=p_{X,Y}(0,0)+p_{X,Y}(1,0)=\frac{1}{2}\frac{1}{4}+\frac{1}{2}\frac{3}{4}=\frac{1}{4}$$

(c)

The expected value of Y is

$$E(Y)=1\cdot p_Y(1)+0\cdot p_Y(0)=\frac{3}{4}$$

(d)

$$E((X-0.5)\times Y)=\sum\limits_{(a,b)}(a-.5)bp_{X,Y}(a,b)$$
$$(1-0.5)(1)p_{X,Y}(1,1)+(1-0.5)(0)p_{X,Y}(1,0)+$$
$$(0-0.5)(1)p_{X,Y}(0,1)+(0-0.5)(0)p_{X,Y}(0,0)=$$
$$\frac{1}{2}\cdot\frac{3}{8}+0-\frac{1}{2}\cdot \frac{3}{8}+0=0$$

 

[PeroK]

Homework Statement:: .
Relevant Equations:: .

View attachment 293161(a)

The probability mass function of X and Y:

$$p_{X,Y}(1,1)= \frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$$
$$p_{X,Y}(1,0)=\frac{1}{2}\cdot \frac{1}{4}=\frac{1}{8}$$
$$p_{X,Y}(0,1)= \frac{1}{2}\cdot \frac{3}{4}=\frac{3}{8}$$
$$p_{X,Y}(0,0)= \frac{1}{2}\cdot \frac{1}{4}=\frac{1}{8}$$

That's not what I get. If $X = 1$, then we toss the unbiased coin (coin 1) again.

 

[docnet]

That's not what I get. If $X = 1$, then we toss the unbiased coin (coin 1) again.

yes! the problem I solved isn't same as the problem in the prompt :(

but don't worry, i think i know what the problem is asking, and how to solve it

 

[docnet]

OK so here's what I have

(a)

$$P_{X,Y}(1,1)=\frac{1}{2}\frac{1}{2}=\frac{1}{4}$$
$$P_{X,Y}(1,0)=\frac{1}{2}\frac{1}{2}=\frac{1}{4}$$
$$P_{X,Y}(0,1)=\frac{1}{2}\frac{3}{4}=\frac{3}{8}$$
$$P_{X,Y}(1,1)=\frac{1}{2}\frac{1}{4}=\frac{1}{8}$$(b)

$$P_X(1)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$$
$$P_X(0)=\frac{3}{8}+\frac{1}{8}=\frac{1}{2}$$
$$P_Y(1)=\frac{3}{8}+\frac{1}{4}=\frac{5}{8}$$
$$P_Y(0)=\frac{1}{8}+\frac{1}{4}=\frac{3}{8}$$

(c)

$$E(Y)=\frac{5}{8}+0\cdot \frac{3}{8}=\frac{5}{8}$$

(d)

$$E((X-.5)\times Y)=(\frac{1}{2}\frac{1}{2}-\frac{1}{2}\frac{1}{2})\frac{5}{8}=0$$

 

[PeroK]

It looks right apart from the answer to d). Note that in general $E(XY) \neq E(X)E(Y)$. (Another simple but erroneous calculation on your part!) But, in general, $E(X + Y) = E(X) + E(Y)$. That gives you two ways to do part d): go through the four options, or use the expected value of a sum.

 

[docnet]

@PeroK thank you :) is this what you mean?

using the formula:
$$E((X-.5)Y)=\frac{1}{8}-\frac{3}{16}=-\frac{1}{16}$$ using linearity and the definition of covariance:

$$E((X-.5)Y)=E(XY)-\frac{5}{16}$$

$$E(XY)=cov(X,Y)+E(X)E(Y)=-\frac{1}{16}+\frac{5}{16}$$

$$E((X-.5) Y)=-\frac{1}{16}$$

 

[PeroK]

Yes, it's good to see you do it both ways and get the same answer!

Note: the quick and valid way to get $E(XY)$ is to note that $XY$ is only non-zero when $X = Y = 1$, which happens with probability $1/4$. Hence $E(XY) = \frac 1 4$.