Why Does the Effective Period of a Composite Wave Remain Constant?

[roam]

TL;DR

I am trying to understand whether the period of a composite wave relates to the relative phases or the number of the constituent waves.

I am working with a simulation which generates multiple identical functions that overlap differently (i.e., they are generated with randomly different phases from each other).

When I calculate the composite wave, the shape of the combined wave will differ depending on the relative phases of the input waves. But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that? What would be an analytic expression that explains this phenomenon?

For instance, this is the simulation using three waves (the thicker line is their sum):

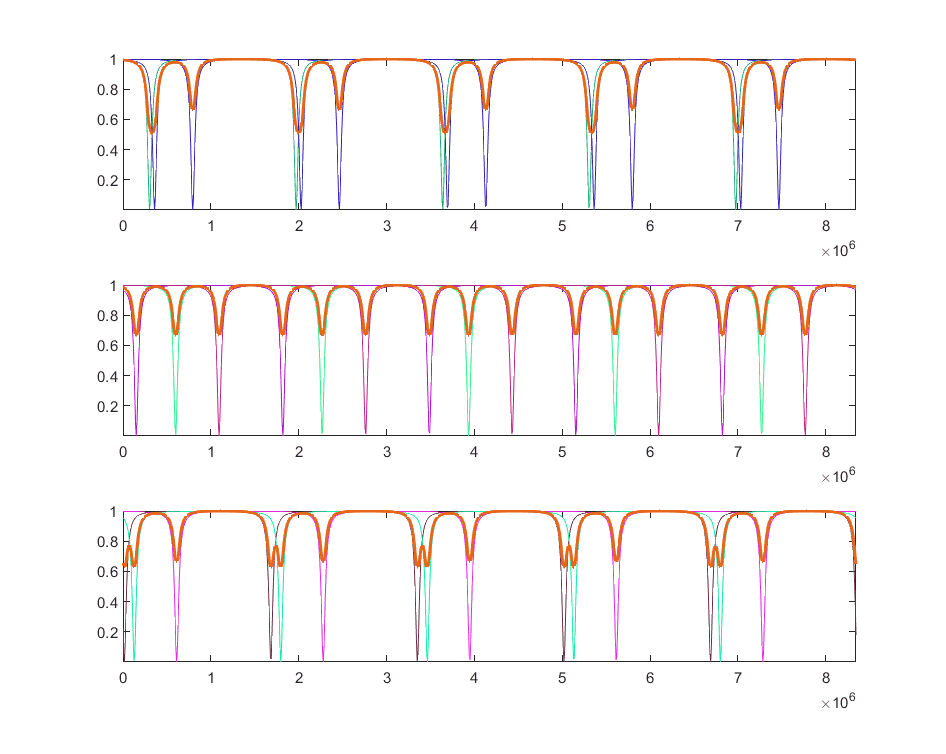
In addition, if we increase the number of waves, the temporal period of the combined wave will still remain constant. Why?

Here is an example:

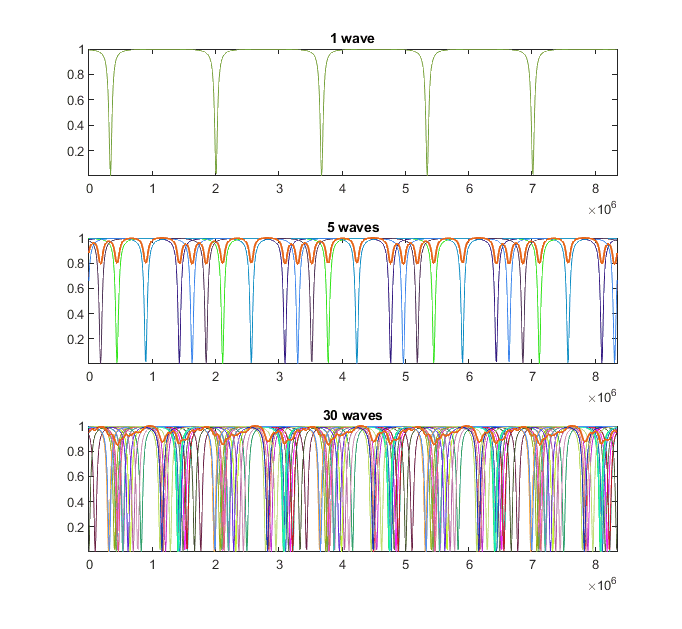
Any explanations would be appreciated.

 

[DrClaude]

I don't understand what these "waves" are. It seems to be simply a peaked function that is repeated periodically.

Also, the thicker line doesn't appear to be the sum of the other curves, but rather the average value of the sum.

When I calculate the composite wave, the shape of the combined wave will differ depending on the relative phases of the input waves. But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that? What would be an analytic expression that explains this phenomenon?

If the underlying phenomena have the same period, then any linear combination of them will have the same period.

 

[roam]

Hi DrClaude,

I don't understand what these "waves" are. It seems to be simply a peaked function that is repeated periodically.

Also, the thicker line doesn't appear to be the sum of the other curves, but rather the average value of the sum.

The function I am using is the complementary Airy function that gives the ratio of light reflected from an interferometer.

The thick line is the normalized sum of the individual curves.

If the underlying phenomena have the same period, then any linear combination of them will have the same period.

Do you know of an analytic expressions that shows that the combination will always have the same period (regardless of the phases or the number of the individual constituents)?

 

[DrClaude]

Consider a set of functions $\{ f_i(x) \}$ of period $a$, i.e., $f_i(x+a) = f_i(x)$. Taking $F(x)$ as a linear combination of such functions,
$$
F(x) = \sum_{i=1}^{n} c_i f_i(x)
$$
then
$$
F(x+a) = \sum_{i=1}^{n} c_i f_i(x+a) = \sum_{i=1}^{n} c_i f_i(x) = F(x)
$$
therefore $F(x)$ is periodic with period $a$.

 

[sophiecentaur]

I would say that the 'period' of a periodic function is (strictly) the interval between points when the waveform repeats. If the waveform consists of a number of functions, each of which has its own identifiable period (sine waves or strings of pulses, for instance), then the period of the composite function would be the lowest common multiple of the individual functions. This could be a very long period if the periods have, say periods of large prime numbers of seconds. This would, for instance, correspond to the 'beat' between two sine waves.

 

[jbriggs444]

This could be a very long period if the periods have, say periods of large prime numbers of seconds.

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

 

[roam]

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

This is an interesting point. So, if there are more than two individual signals present, then the ratio of the periods of each pair of signals must be rational. Otherwise, the signal will not be periodic. Is that correct?

Also, do you think this happens often in real life where the two signals have incommensurable periods?

 

[sophiecentaur]

If the ratio of the periods of the individual functions is an irrational number, their sum may not be periodic at all.

I don’t think the term “irrational” is applicable here.
“Irrational” measurements don’t occur. All you can expect is a long recurrence in the ratio of the periods. (Longer than any possible experiment could last.)

 

[DrClaude]

I don’t think the term “irrational” is applicable here.
“Irrational” measurements don’t occur. All you can expect is a long recurrence in the ratio of the periods. (Longer than any possible experiment could last.)

Oh, come on! Who said anything about measurements? This is about the sum of mathematical functions.

 

[sophiecentaur]

Oh, come on! Who said anything about measurements? This is about the sum of mathematical functions.

I have to agree. But the OP is discussing numerical simulation, which is where I got the idea of practicality.

 

[roam]

I am simulating a physical situation where optical fibers can host more than one spatial modes. From what I understood, if you don't experimentally see a period to such a signal on an oscilloscope, it could be the case that the ratio of the period of the constituent modes is not rational (or rather it has a longer recurrence than the length of the experiment).

 

[sophiecentaur]

not rational (or rather it has a longer recurrence than the length of the experiment)

Bearing in mind that you can't produce irrational numbers in a numerical simulation, we should settle for 'a very long repeat time', I think.

 

[jbriggs444]

the ratio of the periods of each pair of signals must be rational. Otherwise, the signal will not be periodic. Is that correct?

For all practical purposes, yes, that would be correct.

Mathematically, there is a loophole. Suppose that you have two signals with period x that sum to zero and a third signal with period kx for some irrational number k. Then the sum of all three signals will be periodic despite two component signals having periods with an irrational ratio.

 

[sophiecentaur]

I think we’re in the fuzzy, oxymoron region here - between axiomatic arguments and practical experience. I don’t Think the thread can reveal much more.

 

[Dullard]

I'm still trying yo figure out how a ratio could ever be 'irrational.'

 

[DrClaude]

I'm still trying yo figure out how a ratio could ever be 'irrational.'

What about $\sqrt{2}/2$?

 

[Dullard]

OK. I should have said: A ratio of periods. Can the period of a waveform be irrational?

 

[DrClaude]

OK. I should have said: A ratio of periods. Can the period of a waveform be irrational?

See for instance
https://www.physicsforums.com/threa...give-incommensurate-potential-periods.968851/

 

[sophiecentaur]

What about $\sqrt{2}/2$?

Point!

 

[sophiecentaur]

What about $\sqrt{2}/2$?

In the case of a one dimensional quantity like frequency, is there a way that an irrational frequency can occur? You can get a line that is 'exactly' √2 inches long but only in a two dimensional figure.
Also, I was thinking about transcendental numbers like e and π. Apart from passing through values involving, say e, can you get a steady frequency of e X 10⁶ Hz? This is a question for someone well versed in Analysis, I think.

 

[jbriggs444]

In the case of a one dimensional quantity like frequency, is there a way that an irrational frequency can occur?

If we grant the assumption that frequencies are precisely knowable then the natural assumption would be that irrational frequencies are the norm and that rational frequencies are the exception. Viewed on a one-dimensional dartboard of real numbers, the rational numbers are a target set of measure zero.

But let us make it practical. If I have a piano string with a density of 2 grams per centimeter and a second piano string with a density of 1 gram per centimeter with both strings the same length and tension then the ratio of the frequencies should be $\frac{\sqrt{2}}2$

Assuming I am not being a bonehead interpreting the string frequency formula.

 

[Paul Colby]

I am simulating a physical situation where optical fibers can host more than one spatial modes. From what I understood, if you don't experimentally see a period to such a signal on an oscilloscope, it could be the case that the ratio of the period of the constituent modes is not rational (or rather it has a longer recurrence than the length of the experiment).

Okay, so optical frequencies are like $10^{14}$ hertz or more. My scope cuts out around $10^8$ Hertz. Can I ask where you purchased yours?

 

[sophiecentaur]

If we grant the assumption that frequencies are precisely knowable then the natural assumption would be that irrational frequencies are the norm and that rational frequencies are the exception.

But let us make it practical. If I have a piano string with a density of 2 grams per centimeter and a second piano string with a density of 1 gram per centimeter with both strings the same length and tension then the ratio of the frequencies should be $\frac{\sqrt{2}}2$

Assuming I am not being a bonehead interpreting the string frequency formula.

I can see where you're coming from and the Maths makes you right but you are talking in purely theoretical terms.
I seem to remember that , from Archimedes, it can be shown that between any two rational numbers there will always be an irrational number which lies in between them. So with your Maths hat on, you have to be right. This implies that signals of any two frequencies, generated totally independently, would have an indeterminately long repeat period.
Frequencies, generated from the same frequency reference, will have rational values (on that reference scale), though.

 

[jbriggs444]

it can be shown that between any two rational numbers there will always be an irrational number which lies in between them

Yes. And vice versa. Both the rationals and the irrationals are dense in the reals. No matter where you land a dart, there will be both irrational and rational numbers arbitrarily close.

From a practical point of view, this means that in any experiment with any margin of error, no matter how small, the measured result will be consistent with infinitely many true values that are rational and infinitely many true values that are irrational. [Making the notion of a "true value" rather questionable].

But that takes all the fun out of the game. So I'm putting my funny looking math hat back on.

 

[sophiecentaur]

So I'm putting my funny looking math hat back on.

I know a number of Maths teachers and worked with a number of Mathematicians. They were nice people but slightly (in some cases, even more than slightly) nutty. I think the subject has a way of getting its own back on Mathematicians. How can you be rational when at least half of the stuff you are dealing with is irrational?

 

[Paul Colby]

In many ways, periodic functions are a fiction, a useful mathematical abstraction used to describe nature under limited circumstance. Since the universe is finite in time, there are no truly periodic functions.

 

[tade]

But regardless of how the waves overlap, the "effective period" of the combined wave seems to remain the same. Why is that?

The good doctor has already explained it, but anyway, to the contrary, you should expect the effective period to remain the same, and in fact, it would be very surprising if it didn't.

 

[Paul Colby]

I don't know about anyone else, but the question raised in #2 wasn't addressed AFAIK. A reflection coefficient is not a wave. What's plotted in #1 appears to be the magnitude of the reflection (transmission?) coefficient for X where X is what exactly?

 

[sophiecentaur]

I don't know about anyone else, but the question raised in #2 wasn't addressed AFAIK. A reflection coefficient is not a wave. What's plotted in #1 appears to be the magnitude of the reflection (transmission?) coefficient for X where X is what exactly?

You're right. If there's reflection then the time and spatial variations come into it. Or is it just the repeating interference pattern due to two signal paths that's being discussed? I don't see how any such diffraction patterns will ever repeat over a wide angle.

 

[Paul Colby]

Yeah, I agree. The reason to ask is this impacts what operations are done on said "signal". Looks like maybe a scanning fiber interferometer of some sort where (I'm guessing) the "waves" are fiber modes. A great deal more need be supplied IMO.