The Potential of Back-to-Back Photons: an Experiment

[Grelbr42]

TL;DR

Back to back photons in coincidence detector

In some cases, photons can be produced in "back to back" (BTB) conditions. For example, electron-positron annihilation produces two photons, each at 0.511 MeV, with equal and opposite momentum. Or pretty close, up to the original velocities of the electron and positron.

Start with a source of such BTB photons. Put it at the middle of a sphere of detectors. It should produce a uniform probability of photons anywhere in that sphere. Now put some diffraction barriers on one side. For example, if you put in a ring you should be able to produce a situation where the signal is higher through the center of the ring. It should be brighter at the center than without the ring.

So, crank down the intensity until you can discern which photons belong together. When a photon is detected at some location, the paired photon should be detected at the same time.

Now save only photon pairs such that one photon arrives at the "bright spot" at the right, and the other arrives anywhere.

Brace yourself for my poor artistic style. It should look something like so.

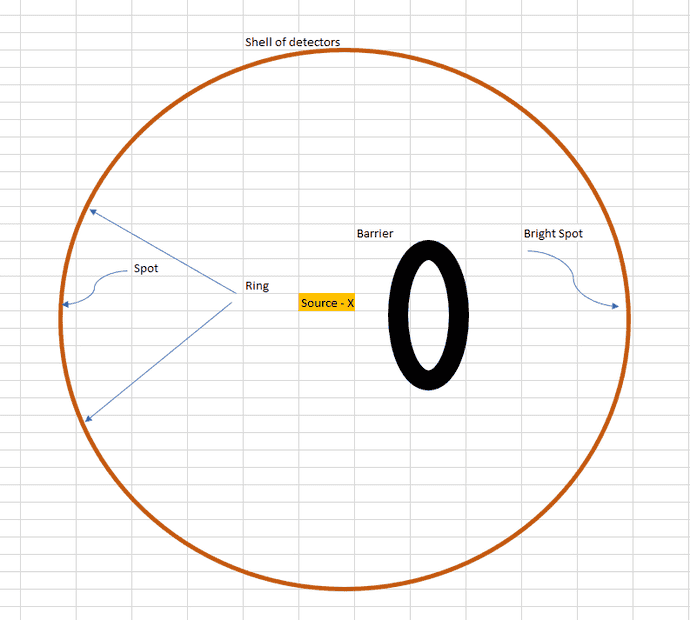
So there should be a spot on the left side corresponding to photons that "went straight through" the diffraction barrier. But there should also be a ring of photons on the left side corresponding to photons that got diffracted to the bright spot on the right.

So, without the diffraction barrier, the paired photons should be completely back-to-back. But with it, and saving only those such that one arrives at the bright spot at the right, then on the left there should be a dot and a ring.

Has such an experiment ever been done? And is my estimation of what would be the result correct?

 

[Dale]

What you describe is PET imaging. However, at 511 keV the wavelength is substantially smaller than a single atom. So diffraction is essentially nonexistent.

 

[Grelbr42]

Thank you Dale! I learned something today.

Indeed, reading the Wikipedia article tells me a lot of cool info.

https://en.wikipedia.org/wiki/Positron_emission_tomography

The patient takes a dose of a substance that emits positrons. These then migrate through the body. The scanner then detects paired photons. The path of the paired photons gives a line on which the positron was emitted. And the difference in arrival time between the two ends gives the position along that line. Thus a 3-D image is possible.

By selecting source isotopes of different chemical elements, it is possible to tailor source molecules that will tend to migrate to the portion of the body of interest. The result is that tissue can be imaged with lower overall dose and higher resolution.

In addition to imaging, it is possible to trace the process of various chemicals through the tissue. One application is that the efficiency of drugs getting to where they are needed can be measured. It lets drugs be modified so they go more where they are needed and less where they are not needed.

Very cool!

 

[Grelbr42]

So, follow-on question. Is there a convenient source of paired photons at lower energy? Say somewhere from visible light to microwaves? Lower energy photons means no dose and possibly some diffraction.

 

[Dale]

Not that I know of, but my expertise is in medical imaging. There may be some quantum mechanical sources that I don’t know about