The prism is made from glass and its cross section is an

[atoreta88]

Homework Statement

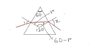
the prism is made from glass, and its cross section is an equilateral triangle. the indices of refraction for the red and violet light are 1.662 and 1.698, respectively. the angle of incidence for both the red and violet light is 60 degrees. find the angles of refraction at which the red and violet rays emerge into the air from the prism

Homework Equations

I know I'm supposed to use the formula n1*sin theta 1=n2 *sin theta 2.

The Attempt at a Solution

I tried plugging in 60 degrees into theta 1, and i tried plugging n1 and n2 with the indices of refractions that are given. then using all those knowns i tried to solve for the unknown, theta 2, but it didn't give me the right answer. my answer was close, but it's not correct.

 

[Swap]

you have to do a bit of geometry here first. see the attachment. U can find r by the formula u stated. Then use sin(60-r)/sin(x)=1/n to find the angle x at which they emerge. You have to do separately for the red and violet but using the same process