The relation between the normal and the slope of a cylindrical curve

[baby_1]

As you can see in this picture:

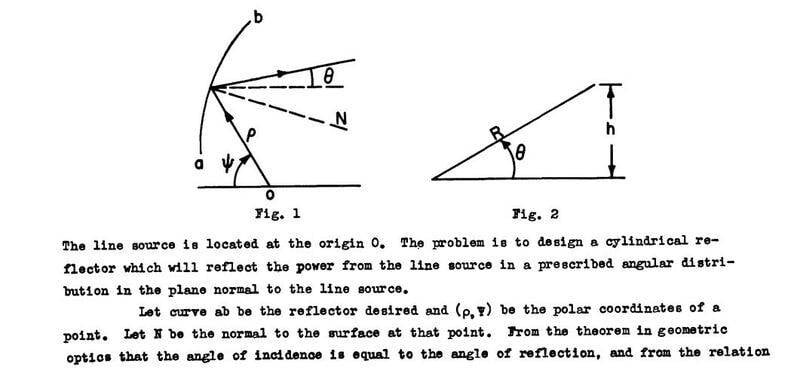This explanation "relation between the normal and the slope of a curve" is formulated here:

$$\frac{1}{\rho} \frac{d\rho }{d\psi }=\tan\left(\frac{\theta+\psi}{2}\right)$$

I got confused because I don't have the curve equation(regarding the slope of the curve and normal vector) and I am curious to know how the above equation is derived.

First I assume that the normal vector on cylindrical curve is going to obtain via gradian operator:
$$\bigtriangledown F=\frac{\partial F }{\partial r}\hat{ar}+\frac{\partial F }{r\partial \phi}\hat{\phi}+\frac{\partial F }{\partial z}\hat{az}$$
but I don't have the F function, and as you can see the above question the writer assume F as $$\rho$$ that I don't understand where it comes from and why the writer used the only phi component.

I will be grateful if you could help me to obtain the formula based on the curve coordinates.

 

[malawi_glenn]

@baby_1 what has this to do with textbooks?

 

[baby_1]

Thank you Malawi_glenn,
Yes, it seems the administrators changed the group of my question. My question is part of an article instead of a textbook.