The smallest circle that two parts of a semi-circle can fit into?

  • Context: MHB 
  • Thread starter Thread starter TrevorE
  • Start date Start date
  • Tags Tags
    Circle Fit parts
Click For Summary
SUMMARY

The discussion centers on determining the smallest circle that can contain two parts of a semi-circle, specifically when cutting a circular tortilla. Three optimal solutions are proposed: the first requires a straight-line cut from the center to the edge, the second allows for any division of the semi-circle, and the third permits non-linear cuts. The suggested method for achieving the smallest plate size involves drawing a circle with a radius of $\frac{r}{\sqrt{2}}$ and consuming the annulus first, leaving minimal leftovers.

PREREQUISITES
  • Understanding of basic geometry concepts, particularly circles and semi-circles.
  • Familiarity with mathematical notation and expressions, such as radius and annulus.
  • Knowledge of optimization techniques in geometric contexts.
  • Ability to visualize geometric transformations and cuts.
NEXT STEPS
  • Explore geometric optimization problems involving circles and semi-circles.
  • Research the properties of annuli and their applications in geometry.
  • Learn about mathematical proofs related to circle packing and minimal enclosing shapes.
  • Investigate non-linear cutting techniques in geometric shapes for practical applications.
USEFUL FOR

Mathematicians, geometry enthusiasts, culinary artists interested in food presentation, and anyone involved in optimization problems related to shapes and space utilization.

TrevorE
Messages
1
Reaction score
0
So, true story:

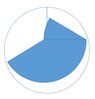
I made a large circular tortilla.

Ate half of it. Then decided to put the rest into the fridge on a smaller plate.I raised the knife to cut the remaining semi-circle in two, and then went : "Hmmmmmmmm...".

Anyway, it's in the fridge now with an approximate solution, but I'm wondering if anyone knows the mathematical one?

I'm wondering if there are 3 different optimal solutions:

1) In which the straight-line cut necessarily is from the center of the original circle to the edge. I.e. a radius.
2) In which the straight-line cut may divide the semi-circle in any possible way.
3) In which the cut is not necessarily a straight line.

Thanks in advance if anyone can offer a demonstration.View attachment 9517
 

Attachments

  • Capture.JPG
    Capture.JPG
    33.8 KB · Views: 132
Last edited:
Mathematics news on Phys.org
Next time, don't cut it that way. Instead, draw a circle on your pizza with radius $\frac r {\sqrt 2}$ and eat the annulus for your first half. You will be left with the smallest possible plate size.
 

Similar threads

Undergrad Can chatgpt accurately calculate expected lengths in Pascal's triangle?
  • · Replies 66 ·
3
Replies
66
Views
7K
Bio-Savart Law, current through wire in semi circle
  • · Replies 2 ·
Replies
2
Views
5K
Graduate Minimum boundary when dividing eqilateral triangle in 4 equal sized parts
  • · Replies 2 ·
Replies
2
Views
5K
MHB How Can One Demonstrate the Ratio Between the Hypotenuses of Two Triangles?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Existence of point(s) within k distance of other fixed points
  • · Replies 3 ·
Replies
3
Views
2K
Graduate Can one divide a circle into 9 areas without the areas being equal?
  • · Replies 15 ·
Replies
15
Views
10K
Undergrad What is the Solution to the Overlapping Circles Number Problem?
  • · Replies 4 ·
Replies
4
Views
4K
Evaluating Line Integral for xy Plane Semi-Circle
  • · Replies 4 ·
Replies
4
Views
4K
Underground pump vault airflow considerations
  • · Replies 15 ·
Replies
15
Views
4K
Prove Infinitely Many Points w/ Equal Dist from x,y in Euclidean Space
  • · Replies 1 ·
Replies
1
Views
2K