Thermodynamic cycle efficiency

In summary, the problem is to calculate the efficiency of a circular cycle using n moles of gas that follow the van der Waals equation. The cycle is represented on a T-S diagram using T_h and T_c as parameters. The idea is to divide the circle into two curves and use the equation Q = TdS to integrate over the top and bottom curves to obtain Q_(in) and Q_(out), respectively. The efficiency can then be calculated using the equation above. However, the challenge lies in calculating the integrals with only the van der Waals equation initially given. The original diagram was an ellipse, but it was clarified that the task states a circle must be used. The units of T and S are different,
  • #1
TK421
4
0

Homework Statement


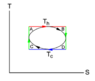
n moles of gas, that follow van der Waals equation are to be employed as the auxiliary system in a circular cycle(parameterized using T_h and T_c as shown on the TS diagram. Calculate the efficiency of the cycle.
300px-Carnot_cycle_TS.png

Homework Equations


dd3272a14ad6d40a0c7043c59febef22a36554e3
,
443830ab2a64edf2fbda997450e2e19e637c7849
, Q = TdS

The Attempt at a Solution


Idea is simple. I just divide circle curve horizontally in two two curves. Using Q = TdS , by integration over the top curve i obtain Q_(in), by integrating over the bottom curve i obtain Q_(out). Then i easily get efficiency using equation above. The only problem is, that i don't know, how to calculate those integrals with only van der Waals equation of state initially given.
 

Attachments

  • 300px-Carnot_cycle_TS.png
    300px-Carnot_cycle_TS.png
    3.1 KB · Views: 695
Physics news on Phys.org
  • #2
What is the equation for the area of an ellipse in terms of the semi major and semi minor axes?
 
  • #3
Sorry, I wasn't precise enough, it has to be a circle, not an ellipse. I put that diagram more for an illustrative purpose.
 
  • #4
TK421 said:
Sorry, I wasn't precise enough, it has to be a circle, not an ellipse. I put that diagram more for an illustrative purpose.
How can it be a circle if the units are different? If you change the units of either T or S, the shape changes.
 
  • #5
Absolutely.
The task itself states, that we are given a cycle, which is represented as a circle on a T-S diagram, which is parameterized using T_h and T_c.
My main concern though is, how would i get an expression of T as a function of S...
 
  • #6
TK421 said:
Absolutely.
The task itself states, that we are given a cycle, which is represented as a circle on a T-S diagram, which is parameterized using T_h and T_c.
My main concern though is, how would i get an expression of T as a function of S...
$$\left(\frac{T-\frac{(T_H+T_C)}{2}}{\frac{(T_H-T_C)}{2}}\right)^2+\left(\frac{S-\frac{(S_{max}+S_{min})}{2}}{\frac{(S_{max}-S_{min})}{2}}\right)^2=1$$
 
  • #7
Like I said, since T and S have different units, you can't represent the variation as a circle on a T-S diagram. What don't you understand about this?
 
  • #8
I do understand it now. Thank you :)
 
  • #9
TK421 said:
I do understand it now. Thank you :)
So what do you get for the efficiency?
 

1. What is thermodynamic cycle efficiency?

Thermodynamic cycle efficiency refers to the ratio of the work output of a thermodynamic cycle to the energy input. It is a measure of how efficiently a cycle converts input energy into output work.

2. How is thermodynamic cycle efficiency calculated?

Thermodynamic cycle efficiency is calculated by dividing the work output by the energy input. It is typically expressed as a percentage and can be calculated for various types of thermodynamic cycles, such as the Carnot cycle or the Rankine cycle.

3. What factors affect thermodynamic cycle efficiency?

Several factors can affect thermodynamic cycle efficiency, including the type of cycle, the temperature and pressure of the working fluid, and the efficiency of individual components such as turbines and compressors. External factors such as heat loss and friction can also impact efficiency.

4. Why is thermodynamic cycle efficiency important?

Thermodynamic cycle efficiency is important because it measures the effectiveness of a thermodynamic system in converting energy into useful work. Higher efficiency means less energy is wasted and more work is produced, resulting in cost savings and reduced environmental impact.

5. How can thermodynamic cycle efficiency be improved?

There are several ways to improve thermodynamic cycle efficiency, such as using higher quality components, reducing heat loss, and optimizing the temperature and pressure of the working fluid. Another approach is to use waste heat recovery systems to capture and reuse energy that would otherwise be lost.

Similar threads

Heat engine that uses a rubber band (Thermodynamics)
    • Advanced Physics Homework Help
Replies
2
Views
1K
B Heat pump as a heat engine that operates in reverse
    • Thermodynamics
Replies
3
Views
567
Question about Reversible Engines and Carnot Efficiency
    • Advanced Physics Homework Help
Replies
6
Views
2K
Closed cycle of an ideal gas
    • Introductory Physics Homework Help
Replies
3
Views
142
Heat engine undergoing an elliptical cycle
    • Advanced Physics Homework Help
Replies
5
Views
1K
Is the Entropy in a Free Expansion Affected by the Gas Type?
    • Advanced Physics Homework Help
Replies
8
Views
2K
Equilibrium volume of two differential van der Waal gases
    • Advanced Physics Homework Help
Replies
7
Views
2K
Relation between heat capacities and van der Waals equation
    • Advanced Physics Homework Help
Replies
23
Views
9K
Temperatures of the hot source and cold sink in a heat engine
    • Thermodynamics
Replies
2
Views
1K
Adiabatic process of real gas
    • Advanced Physics Homework Help
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top