- #1
Tethys
- 7
- 0
Hello! I've been a long-time follower of the Physics Forums and have found it to be a great resource for a variety of physics and engineering topics, although I have not actually felt compelled to create an account on the boards until today. I have encountered a difficult thermodynamics problem in a homework assignment that I would like some input on. I have changed some of the numbers from the original problem because I would like to actually solve the given problem myself, but the concepts are the same.
Relevant equations
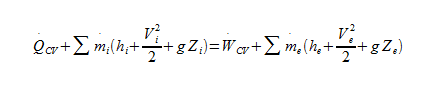
Part One of the Problem
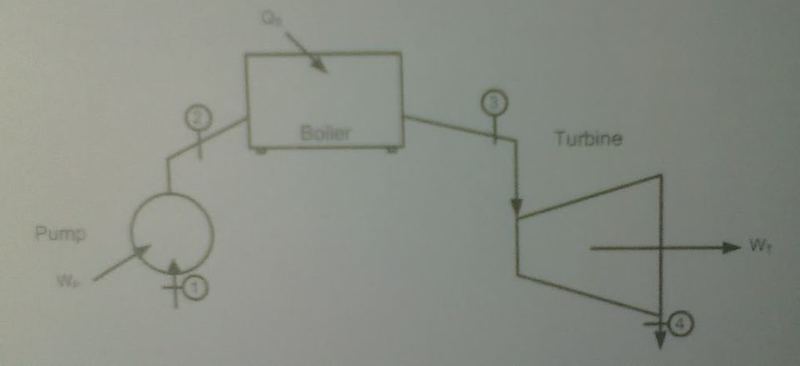
Water passes through a pump in a steady-state process in which there is no height change, no heat transfer, and a constant temperature across the device. The water initially has a pressure of 15 kPa and a temperature of 53.97 C, and it leaves the pump with an exit pressure of 5MPa. How much work is required to pressurize the water if the mass flow rate through the pump is 25 kg/s? Define the phase of the water at State 1 and State 2, and draw the process on a T-v diagram (v is specific volume).
Part Two of the Problem
The water is converted into steam in a constant-pressure process after exiting the high-pressure pump. How much heat is transferred to the water if the steam temperature is 500 C coming out of the bioler? What is the phase of the water at State 3? Draw the process on a T-v diagram.
Part Three of the Problem
Compute the turbine work output and draw the T-v diagram if the exit velocity from the turbine is 150 m/s and the steam expands through the turbine until it is saturated water at 15 kPa and 90% quality.
Much thanks in advance for the help and input,
-Tethys
Relevant equations
Part One of the Problem
Water passes through a pump in a steady-state process in which there is no height change, no heat transfer, and a constant temperature across the device. The water initially has a pressure of 15 kPa and a temperature of 53.97 C, and it leaves the pump with an exit pressure of 5MPa. How much work is required to pressurize the water if the mass flow rate through the pump is 25 kg/s? Define the phase of the water at State 1 and State 2, and draw the process on a T-v diagram (v is specific volume).
Part Two of the Problem
The water is converted into steam in a constant-pressure process after exiting the high-pressure pump. How much heat is transferred to the water if the steam temperature is 500 C coming out of the bioler? What is the phase of the water at State 3? Draw the process on a T-v diagram.
Part Three of the Problem
Compute the turbine work output and draw the T-v diagram if the exit velocity from the turbine is 150 m/s and the steam expands through the turbine until it is saturated water at 15 kPa and 90% quality.
Much thanks in advance for the help and input,
-Tethys