Is My Calculation for Bicycle Pump Pressure Incorrect?

[Hak]

Homework Statement

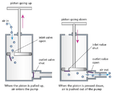
A bicycle wheel pump works as shown in the figure below. When you pull up on the pump knob, the cylindrical barrel of the pump fills with air from the outside, which enters through a one-way valve. When the knob is pushed down, the air compresses into the tube until its pressure reaches that of the inner tube connected to the pump. At that point, another one-way valve allows air to go from the pump into the inner tube.

Assume that any compression is isothermal, as if you push the knob very slowly, so that the temperature remains in equilibrium with the external environment. Assume also that there is no air leakage from either the pump or the inner tube.

The volume of a pump barrel is $$\displaystyle V_P = 0.3$$ liters; the pump is connected to an air chamber of volume $$\displaystyle V_C = 4.5$$ liters. Assume that the air chamber is inflexible, so its volume does not increase significantly while inflating it. Initially, the pressure in the air chamber equals the atmospheric pressure $$\displaystyle p_A = 101.3$$ kPa.

1.) Using the pump, push the knob down and then up 4 times, so you transfer air 4 times from pump to inner tube. After you do this, what is the pressure in the inner tube?
2.) You might imagine that you have a pump 4 times the size of the one you have, with which you would only have to press down on the knob once to fill the inner tube. If $$\displaystyle W_1$$ is the work done to fill the inner tube with four compressions of the small pump and $$\displaystyle W_2$$ that of the air pump, how much extra work is worth required in the first case, $$\displaystyle W_2 - W_1$$?

Relevant Equations

/

The pressure in the inner tube after four transfers of air from the pump is given by the formula:

$$\displaystyle p_C = p_A \left(\frac{V_C + V_P}{V_C}\right)^n$$

where $$\displaystyle n$$ is the number of transfers, $$\displaystyle p_C$$ is the pressure in the inner tube, $$\displaystyle p_A$$ is the atmospheric pressure, $$\displaystyle V_C$$ is the volume of the inner tube, and $$\displaystyle V_P$$ is the volume of the pump.

Plugging in the given values, we get:

$$\displaystyle p_C = 101.3 \left(\frac{4.5 + 0.3}{4.5}\right)^4$$

$$\displaystyle p_C = 101.3 \times 1.0667^4$$

$$\displaystyle p_C = 101.3 \times 1.2978$$

$$\displaystyle p_C = 131.4 kPa$$

Therefore, the pressure in the inner tube after four transfers of air from the pump is 131.4 kPa.

2.) The work done by the pump to transfer air from the pump to the inner tube is given by the formula:

$$\displaystyle W = nRT \ln\left(\frac{V_C + V_P}{V_C}\right)$$

where $$\displaystyle n$$ is the number of moles of air, $$\displaystyle R$$ is the gas constant, $$\displaystyle T$$ is the temperature, and $$\displaystyle V_C$$ and $$\displaystyle V_P$$ are the volumes of the inner tube and the pump, respectively

For the small pump, we have:

$$\displaystyle W_1 = nRT \ln\left(\frac{V_C + V_P}{V_C}\right)$$

For the large pump, we have:

$$\displaystyle W_2 = nRT \ln\left(\frac{V_C + 4V_P}{V_C}\right)$$

The difference between these two works is:

$$\displaystyle W_2 - W_1 = nRT \left[\ln\left(\frac{V_C + 4V_P}{V_C}\right) - \ln\left(\frac{V_C + V_P}{V_C}\right)\right]$$

Using the property of logarithms, we can simplify this expression as:

$$\displaystyle W_2 - W_1 = nRT \ln\left(\frac{V_C + 4V_P}{V_C + V_P}\right)$$.

Plugging in the given values, we get:

$$\displaystyle W_2 - W_1 = nRT \ln\left(\frac{4.5 + 4 \times 0.3}{4.5 + 0.3}\right)$$

$$\displaystyle W_2 - W_1 = nRT \ln\left(\frac{5.7}{4.8}\right)$$

$$\displaystyle W_2 - W_1 = nRT \times 0.1698$$

Therefore, the extra work required in using the large pump should be proportional to $nRT \times 0.1698$.

I am not convinced by this process; I think it is wrong. Could you tell me where I am wrong? Do you have any suggestions or help? I had thought of a method where you could use the polytropic index of compression, setting it equal to 1 in the case of isothermal compression, but I can't physically formalize it.

 

[erobz]

@Hak whenever you are enumerating the variables try to do that in-line like:

• Let the volume be $V$
• The work is $W$
• …

You don’t have to do bullets, I was just showing you how it reads better when they are compact.

 

[Chestermiller]

I'm not sure I would come up the same answers if I did it my way. Let $m_p$ be the number of moles of air injected from the pump in each stroke and $m_0$ be the initial number of moles of air in the chamber. Then $$m_p=\frac{P_{atm}V_p}{RT}$$ and $$m_0=\frac{P_{atm}V_C}{RT}$$After the nth stroke, the number of moles in the chamber is $$m_n=\frac{P_{atm}V_C}{RT}+n\frac{P_{atm}V_p}{RT}=\frac{P_{atm}(V_C+nV_p)}{RT}$$and the pressure in the chamber after n strokes is $$P_n=\frac{m_nRT}{V_C}=P_{atm}\frac{(V_C+nV_p)}{V_C}$$
This already differs from what you obtained.

Each stroke n involves 2 steps.

(1) Compression of the $m_p$ moles in the cylinder from $P_{atm}$ to $P_{n-1}$

(2) Compression of $m_n$ moles in the pump and cylinder from $P_{n-1}$ to $P_n$

The equation for the work in each of these steps is different

 

[Hak]

I'm not sure I would come up the same answers if I did it my way. Let $m_p$ be the number of moles of air injected from the pump in each stroke and $m_0$ be the initial number of moles of air in the chamber. Then $$m_p=\frac{P_{atm}V_p}{RT}$$ and $$m_0=\frac{P_{atm}V_C}{RT}$$After the nth stroke, the number of moles in the chamber is $$m_n=\frac{P_{atm}V_C}{RT}+n\frac{P_{atm}V_p}{RT}=\frac{P_{atm}(V_C+nV_p)}{RT}$$and the pressure in the chamber after n strokes is $$P_n=\frac{m_nRT}{V_C}=P_{atm}\frac{(V_C+nV_p)}{V_C}$$
This already differs from what you obtained.

Thank you very much. I will post my steps later today, which led me to that solution, which I think is wrong. Yours is most likely right. However, what caught my attention is that mine and your result coincide at first order (when applying the binomial formula). Why?

Each stroke n involves 2 steps.

(1) Compression of the $m_p$ moles in the cylinder from $P_{atm}$ to $P_{n-1}$

(2) Compression of $m_n$ moles in the pump and cylinder from $P_{n-1}$ to $P_n$

The equation for the work in each of these steps is different

I did not understand these two steps. Could you explain why you have these two steps? How did you arrive at this formulation? As soon as I understand better, I will try to write down a possible symbolic solution to point 2.) Thank you.

 

[Hak]

@Hak whenever you are enumerating the variables try to do that in-line like:

• Let the volume be $V$
• The work is $W$
• …

You don’t have to do bullets, I was just showing you how it reads better when they are compact.

Thanks, but what "do bullets" mean? Sorry for not understanding.

 

[Juanda]

Thanks, but what "do bullets" mean? Sorry for not understanding.

Writting like this is called "bullet points".

 

[Chestermiller]

Thank you very much. I will post my steps later today, which led me to that solution, which I think is wrong. Yours is most likely right. However, what caught my attention is that mine and your result coincide at first order (when applying the binomial formula). Why?
I did not understand these two steps. Could you explain why you have these two steps? How did you arrive at this formulation? As soon as I understand better, I will try to write down a possible symbolic solution to point 2.) Thank you.

Except for the first stroke (where the initial pressure in the pump and the initial pressure in the container both are1 atm), the. pressure of the air in the pump starts out at 1 atm, but. the pressure in the container starts out at a pressure higher than 1 atm. So, in the first part of the stroke, the gas in the pump is compressed until it is equal to the pressure in the container (with no air flowing into the container): then,, the check valve into the container is able to open and then air is able to flow into the container; during this second part of the stroke, the pressure of the air in the pump and the pressure of the air in the container rise in tandem. So, in summary, there are two distinct parts to the overall stroke, and the equation for the work in each of these two parts is different.

 

[Hak]

Except for the first stroke (where the initial pressure in the pump and the initial pressure in the container both are1 atm), the. pressure of the air in the pump starts out at 1 atm, but. the pressure in the container starts out at a pressure higher than 1 atm. So, in the first part of the stroke, the gas in the pump is compressed until it is equal to the pressure in the container (with no air flowing into the container): then,, the check valve into the container is able to open and then air is able to flow into the container; during this second part of the stroke, the pressure of the air in the pump and the pressure of the air in the container rise in tandem. So, in summary, there are two distinct parts to the overall stroke, and the equation for the work in each of these two parts is different.

Ok. Following your reasoning, the work done by the pump in each stroke is equal to the sum of the work done in the two parts of the stroke. The work done in each part is given by the formula:

$$\displaystyle W = p \Delta V$$

where $\displaystyle p$ is the pressure and $\displaystyle \Delta V$ is the change in volume.

For the first part of the stroke, where the gas in the pump is compressed until it reaches the pressure in the container, we have:

$$\displaystyle W_1 = p_A (V_P - V_1)$$

where $\displaystyle p_A$ is the atmospheric pressure, $\displaystyle V_P$ is the volume of the pump, and $\displaystyle V_1$ is the volume of the gas in the pump when it reaches the pressure in the container.

For the second part of the stroke, where the gas in the pump and the container is compressed together, we have:

$$\displaystyle W_2 = p_{n-1} (V_1 + V_C - V_2 - V_C)$$

where $\displaystyle p_{n-1}$ is the pressure in the container before the stroke, $\displaystyle V_C$ is the volume of the container, and $\displaystyle V_2$ is the volume of the gas in the pump and the container when it reaches the final pressure.

Simplifying this expression, I get:

$$\displaystyle W_2 = p_{n-1} (V_1 - V_2)$$

Therefore, the total work done by the pump in each stroke is:

$$\displaystyle W = W_1 + W_2$$

$$\displaystyle W = p_A (V_P - V_1) + p_{n-1} (V_1 - V_2)$$

To find $\displaystyle V_1$ and $$\displaystyle V_2$$, I could use Boyle’s law, which states that for an isothermal process, $$\displaystyle pV = constant$$.

For $\displaystyle V_1$, we have:

$$\displaystyle p_A V_P = p_{n-1} V_1$$

$$\displaystyle V_1 = \frac{p_A}{p_{n-1}} V_P$$

For $\displaystyle V_2$, we have:

$$\displaystyle p_{n-1} (V_1 + V_C) = p_n (V_2 + V_C)$$

$$\displaystyle V_2 = \frac{p_{n-1}}{p_n} (V_1 + V_C) - V_C$$

Plugging these values into the expression for $\displaystyle W$, I get:

$$\displaystyle W = p_A \left(V_P - \frac{p_A}{p_{n-1}} V_P\right) + p_{n-1} \left(\frac{p_A}{p_{n-1}} V_P - \frac{p_{n-1}}{p_n} (V_P + V_C) + V_C\right)$$

Simplifying this expression further, I get:

$$\displaystyle W = \frac{p_A^2}{p_{n-1}} V_P - \frac{p_{n-1}^2}{p_n} (V_P + V_C) + p_{n-1} V_C$$.

Where am I wrong? Thanks.

 

[Chestermiller]

Ok. Following your reasoning, the work done by the pump in each stroke is equal to the sum of the work done in the two parts of the stroke. The work done in each part is given by the formula:

$$\displaystyle W = p \Delta V$$

This is correct only if the pressure is constant (which it is not). The correct equation for an ideal gas at constant temperature is $$dW=pdV=\frac{mRT}{V}dV=-\frac{mRT}{P}dP$$

 

[Hak]

This is correct only if the pressure is constant (which it is not). The correct equation for an ideal gas at constant temperature is $$dW=pdV=\frac{mRT}{V}dV=-\frac{mRT}{P}dP$$

Thanks. Should I start from that equation and continue with the previous steps?

 

[Chestermiller]

Thanks. Should I start from that equation and continue with the previous steps?

Just do the first two strokes and lets see what you get.

 

[Hak]

Just do the first two strokes and lets see what you get.

The equation for the work done by a gas in an isothermal process is:

$$\displaystyle dW = pdV = \frac{mRT}{V}dV = -\frac{mRT}{P}dP$$

where $\displaystyle m$ is the mass of the gas, $\displaystyle R$ is the gas constant, and $\displaystyle T$ is the temperature.

This equation can be derived from the ideal gas law, which states that:

$$\displaystyle PV = nRT$$

where $\displaystyle n$ is the number of moles of gas.

If we divide both sides by $\displaystyle n$, we get:

$$\displaystyle \frac{PV}{n} = RT$$

Since $\displaystyle n$ is constant, we can write:

$$\displaystyle \frac{P}{n}dV + \frac{V}{n}dP = 0$$

Multiplying both sides by $$\displaystyle nR$$, we get:

$$\displaystyle PdV + VdP = 0$$

To find the work done by a gas in an isothermal process, I integrate both sides of this equation from an initial state to a final state. I get:

$$\displaystyle W = \int_{V_i}^{V_f} PdV + \int_{P_i}^{P_f} VdP = 0$$

We can simplify this equation by using the ideal gas law to eliminate one of the variables. For example, we can write:

$$\displaystyle P = \frac{mRT}{V}$$

and substitute it into the first integral. We get:

$$\displaystyle W = \int_{V_i}^{V_f} \frac{mRT}{V} dV + \int_{P_i}^{P_f} VdP$$

The first integral can be easily solved by using the power rule. We get:

$$\displaystyle W = mRT \int_{V_i}^{V_f} \frac{1}{V} dV + \int_{P_i}^{P_f} VdP$$

[tex]\displaystyle W = mRT \left[\ln(V)\right]_{V_i}^{V_f} + \int_ {P_i}^{P_f} VdP [/tex]

$$\displaystyle W = mRT (\ln(V_f) - \ln(V_i)) + \int_{P_i}^{P_f} VdP$$

Using the property of logarithms, we can write:

$$\displaystyle W = mRT \ln\left(\frac{V_f}{V_i}\right) + \int_{P_i}^{P_f} VdP$$

This is the expression for the work done by a gas in an isothermal process in terms of volume and pressure.

Alternatively, we can write:

$$\displaystyle V = \frac{nRT}{P}$$

and substitute it into the second integral. We get:

$$\displaystyle W = \int_{V_i}^{V_f} PdV + \int_{P_i}^{P_f} \frac{nRT}{P} dP$$

The second integral can be easily solved by using the power rule. We get:

$$\displaystyle W = \int_{V_i}^{V_f} PdV + nRT \int_{P_i}^{P_f} \frac{1}{P} dP$$

$$\displaystyle W = \int_{V_i}^{V_f} PdV + nRT \left[\ln(P)\right]_{P_i}^{P_f}$$

$$\displaystyle W = \int_{V_i}^{V_f} PdV + nRT (\ln(P_f) - \ln(P_i))$$

Using the property of logarithms, we can write:

$$\displaystyle W = \int_{V_i}^{V_f} PdV + nRT \ln\left(\frac{P_f}{P_i}\right)$$

For the first part of the stroke, where the gas in the pump is compressed until it reaches the pressure in the container, we have:

$$\displaystyle V_i = V_P$$

$$\displaystyle V_f = V_1$$

$$\displaystyle P_i = p_A$$

$$\displaystyle P_f = p_{n-1}$$

where $\displaystyle V_P$ is the volume of the pump, $\displaystyle V_1$ is the volume of the gas in the pump when it reaches the pressure in the container, $\displaystyle p_A$ is the atmospheric pressure, and $\displaystyle p_{n-1}$ is the pressure in the container before the stroke.

For the second part of the stroke, where the gas in the pump and the container is compressed together, we have:

$$\displaystyle V_i = V_1 + V_C$$

$$\displaystyle V_f = V_2 + V_C$$

$$\displaystyle P_i = p_{n-1}$$

$$\displaystyle P_f = p_n$$

where $\displaystyle V_C$ is the volume of the container, $\displaystyle V_2$ is the volume of the gas in the pump and the container when it reaches the final pressure, and $\displaystyle p_n$ is the pressure in the container after the stroke.

To find $\displaystyle V_1$ and $\displaystyle V_2$, we can use Boyle’s law, which states that for an isothermal process, $$\displaystyle pV = constant$$.

For $\displaystyle V_1$, we have:

$$\displaystyle p_A V_P = p_{n-1} V_1$$

$$\displaystyle V_1 = \frac{p_A}{p_{n-1}} V_P$$

For $\displaystyle V_2$, we have:

$$\displaystyle p_{n-1} (V_1 + V_C) = p_n (V_2 + V_C)$$

$$\displaystyle V_2 = \frac{p_{n-1}}{p_n} (V_1 + V_C) - V_C$$

Plugging these values into the expression for $$\displaystyle W$$, I get:

$$\displaystyle W = mRT \ln\left(\frac{V_f}{V_i}\right) + nRT \ln\left(\frac{P_f}{P_i}\right)$$

For each part of the stroke, we can substitute the corresponding values of $\displaystyle V_i$, $\displaystyle V_f$, $\displaystyle P_i$, and $\displaystyle P_f$. We get:

For part 1:

$$\displaystyle W_1 = mRT \ln\left(\frac{V_1}{V_P}\right) + nRT \ln\left(\frac{p_{n-1}}{p_A}\right)$$

For part 2:

$$\displaystyle W_2 = mRT \ln\left(\frac{V_2 + V_C}{V_1 + V_C}\right) + nRT \ln\left(\frac{p_n}{p_{n-1}}\right)$$

Therefore, the total work done by the pump in each stroke is:

$$\displaystyle W = W_1 + W_2$$.

Where am I wrong?

 

[Chestermiller]

The equation for the work done by a gas in an isothermal process is:

$$\displaystyle dW = pdV = \frac{mRT}{V}dV = -\frac{mRT}{P}dP$$

where $\displaystyle m$ is the mass of the gas, $\displaystyle R$ is the gas constant, and $\displaystyle T$ is the temperature.

This equation can be derived from the ideal gas law, which states that:

$$\displaystyle PV = nRT$$

where $\displaystyle n$ is the number of moles of gas.

If we divide both sides by $\displaystyle n$, we get:

$$\displaystyle \frac{PV}{n} = RT$$

Since $\displaystyle n$ is constant, we can write:

$$\displaystyle \frac{P}{n}dV + \frac{V}{n}dP = 0$$

Multiplying both sides by $$\displaystyle nR$$, we get:

$$\displaystyle PdV + VdP = 0$$

To find the work done by a gas in an isothermal process, I integrate both sides of this equation from an initial state to a final state. I get:

$$\displaystyle W = \int_{V_i}^{V_f} PdV + \int_{P_i}^{P_f} VdP = 0$$

This is incorrect. See the equation(s) I wrote in my previous post. Also, I used the symbol m to represent moles, not mass.

First stroke: In this stroke, the pressure in the pump and the pressure in the container start out equal. The starting volume is $V_C + V_p$, and the final volume is $V_C$. So $$W=(m_p+m_{C_{initial}}){RT}\ln{\frac{V_C}{V_C+V_p}}$$Also, from the ideal gas law $$(m_p+m_{C_{initial}})RT=P_{atm}(V_C+V_p)$$So the work in stroke 1 is given by $$W_1=P_{atm}(V_C+V_p)\ln{\frac{V_C}{V_C+V_p}}$$Finally, the pressure in the container at the end of stroke 1 is: $$ P_1=P_{atm}\frac{V_C+V_p}{V_C}$$

STROKE 2
In the first step of stroke 2, the gas is compressed until its pressure matches the pressure in the container that existed at the end of stroke 1, $P_1=P_{atm}\frac{V_C+V_p}{V_C}$. By the end of this step, the volume in the pump has been reduced from $V_p$ to $$V_{2a}=V_p\frac{V_C}{(V_C+V_p)}$$So the work to compress the gas in step 2a is given by $$W_{2a}=P_{atm}V_p\ln{\frac{V_C}{(V_C+V_p)}}$$

In the 2nd stroke of step 2, The starting pressure is $P_{atm}\frac{V_C+V_p}{V_C}$, the starting volume is $V_C+V_p\frac{V_C}{(V_C+V_p)}=V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)$, and the final volume is $V_C$. So the work in second step of stroke 2 is $$W_{2b}=[P_{atm}\frac{V_C+V_p}{V_C}][V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)]\ln{\frac{V_C}{V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)}}$$$$=P_{atm}(V_C+2V_p)\ln{\frac{V_C+V_p}{V_C+2V_p}}$$

 

[Hak]

This is incorrect. See the equation(s) I wrote in my previous post. Also, I used the symbol m to represent moles, not mass.

First stroke: In this stroke, the pressure in the pump and the pressure in the container start out equal. The starting volume is $V_C + V_p$, and the final volume is $V_C$. So $$W=(m_p+m_{C_{initial}}){RT}\ln{\frac{V_C}{V_C+V_p}}$$Also, from the ideal gas law $$(m_p+m_{C_{initial}})RT=P_{atm}(V_C+V_p)$$So the work in stroke 1 is given by $$W_1=P_{atm}(V_C+V_p)\ln{\frac{V_C}{V_C+V_p}}$$Finally, the pressure in the container at the end of stroke 1 is: $$ P_1=P_{atm}\frac{V_C+V_p}{V_C}$$

STROKE 2
In the first step of stroke 2, the gas is compressed until its pressure matches the pressure in the container that existed at the end of stroke 1, $P_1=P_{atm}\frac{V_C+V_p}{V_C}$. By the end of this step, the volume in the pump has been reduced from $V_p$ to $$V_{2a}=V_p\frac{V_C}{(V_C+V_p)}$$So the work to compress the gas in step 2a is given by $$W_{2a}=P_{atm}V_p\ln{\frac{V_C}{(V_C+V_p)}}$$

In the 2nd stroke of step 2, The starting pressure is $P_{atm}\frac{V_C+V_p}{V_C}$, the starting volume is $V_C+V_p\frac{V_C}{(V_C+V_p)}=V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)$, and the final volume is $V_C$. So the work in second step of stroke 2 is $$W_{2b}=[P_{atm}\frac{V_C+V_p}{V_C}][V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)]\ln{\frac{V_C}{V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)}}$$$$=P_{atm}(V_C+2V_p)\ln{\frac{V_C+V_p}{V_C+2V_p}}$$

Thanks. However, how should I continue?

 

[Hak]

This is incorrect. See the equation(s) I wrote in my previous post. Also, I used the symbol m to represent moles, not mass.

First stroke: In this stroke, the pressure in the pump and the pressure in the container start out equal. The starting volume is $V_C + V_p$, and the final volume is $V_C$. So $$W=(m_p+m_{C_{initial}}){RT}\ln{\frac{V_C}{V_C+V_p}}$$Also, from the ideal gas law $$(m_p+m_{C_{initial}})RT=P_{atm}(V_C+V_p)$$So the work in stroke 1 is given by $$W_1=P_{atm}(V_C+V_p)\ln{\frac{V_C}{V_C+V_p}}$$Finally, the pressure in the container at the end of stroke 1 is: $$ P_1=P_{atm}\frac{V_C+V_p}{V_C}$$

STROKE 2
In the first step of stroke 2, the gas is compressed until its pressure matches the pressure in the container that existed at the end of stroke 1, $P_1=P_{atm}\frac{V_C+V_p}{V_C}$. By the end of this step, the volume in the pump has been reduced from $V_p$ to $$V_{2a}=V_p\frac{V_C}{(V_C+V_p)}$$So the work to compress the gas in step 2a is given by $$W_{2a}=P_{atm}V_p\ln{\frac{V_C}{(V_C+V_p)}}$$

In the 2nd stroke of step 2, The starting pressure is $P_{atm}\frac{V_C+V_p}{V_C}$, the starting volume is $V_C+V_p\frac{V_C}{(V_C+V_p)}=V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)$, and the final volume is $V_C$. So the work in second step of stroke 2 is $$W_{2b}=[P_{atm}\frac{V_C+V_p}{V_C}][V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)]\ln{\frac{V_C}{V_C\left(\frac{V_C+2V_p}{V_C+V_p}\right)}}$$$$=P_{atm}(V_C+2V_p)\ln{\frac{V_C+V_p}{V_C+2V_p}}$$

I did not understand why, after calculating $W_1$, you mentioned and calculated $p_1$. Also, I did not understand why you said:

I'm not sure I would come up the same answers if I did it my way. Let $m_p$ be the number of moles of air injected from the pump in each stroke and $m_0$ be the initial number of moles of air in the chamber. Then $$m_p=\frac{P_{atm}V_p}{RT}$$ and $$m_0=\frac{P_{atm}V_C}{RT}$$After the nth stroke, the number of moles in the chamber is $$m_n=\frac{P_{atm}V_C}{RT}+n\frac{P_{atm}V_p}{RT}=\frac{P_{atm}(V_C+nV_p)}{RT}$$and the pressure in the chamber after n strokes is $$P_n=\frac{m_nRT}{V_C}=P_{atm}\frac{(V_C+nV_p)}{V_C}$$
This already differs from what you obtained.

Each stroke n involves 2 steps.

(1) Compression of the $m_p$ moles in the cylinder from $P_{atm}$ to $P_{n-1}$

(2) Compression of $m_n$ moles in the pump and cylinder from $P_{n-1}$ to $P_n$

The equation for the work in each of these steps is different

but, however, you did not include this data (such as, $m_n$, $P_{n-1}$ e $P_n$), within the last procedure you described. Sorry if I can't understand it.

 

[TSny]

Note that part (2) of the problem asks only for the difference $W_2 - W_1$ in total work $W_2$ for the large pump and the total work $W_1$ for the four strokes of the small pump. It is possible to deduce $W_2 - W_1$ without having to explicitly calculate the works $W_1$ and $W_2$ individually. Very little calculation is required.

However, it is a nice exercise to follow @Chestermiller 's lead and calculate $W_1$ and $W_2$ individually and then compare them. This is fairly lengthy, but it will get to the answer.

[There is a possibility of confusion with notation. In the statement of the problem $W_1$ is the total work done in performing four consecutive strokes of the small pump. Chestermiller has also used the notation $W_1$ for the work of only stroke 1 of the small pump, as he makes clear. Also, it appears to me that Chestermiller has found expressions for the work done by the air rather than the work done on the air. So, be careful with signs.]

 

[Hak]

Note that part (2) of the problem asks only for the difference $W_2 - W_1$ in total work $W_2$ for the large pump and the total work $W_1$ for the four strokes of the small pump. It is possible to deduce $W_2 - W_1$ without having to explicitly calculate the works $W_1$ and $W_2$ individually. Very little calculation is required.

Could you give me some advice on how to calculate it this way?

[There is a possibility of confusion with notation. In the statement of the problem $W_1$ is the total work done in performing four consecutive strokes of the small pump. Chestermiller has also used the notation $W_1$ for the work of only stroke 1 of the small pump, as he makes clear. Also, it appears to me that Chestermiller has found expressions for the work done by the air rather than the work done on the air. So, be careful with signs.]

In fact, I am very confused. What do 'stroke 1' and 'stroke 2' mean? If 'stroke 1' only refers to the first stroke, $W_1$ would not be the same as the work required by the text as such, right? How is it possible to connect the fact that in the statement of the problem $W_1$ is the total work done in performing four consecutive strokes of the small pump, with the fact that each stroke contains 2 steps within it? I am also confused to understand the difference between the work of the small pump and the work of the large pump: what do @Chestermiller's results refer to, the former, the latter or both? I would be grateful for some clarity, I don't seem to understand much.

 

[Chestermiller]

I did not understand why, after calculating $W_1$, you mentioned and calculated $p_1$.

You need to know the pressure in the container at the end of stroke 1 to (a) find how much you need to. compress the gas in step 1 of stroke 1 and in getting the work for step 2 of stroke 2.

 

[Chestermiller]

Thanks. However, how should I continue?

You do stroke 3 next. This would bedone by the same algorithm as was used for stroke 2. So, just mimic that.

 

[Hak]

You do stroke 3 next. This would bedone by the same algorithm as was used for stroke 2. So, just mimic that.

OK, thank you very much. But how should I indicate the work I find? As I understand it, what you indicated with $W_1$ and $W_2$ are just two of the four strokes of the small pump. How do I calculate the work of the big pump?

 

[TSny]

Could you give me some advice on how to calculate it this way?

Let's clearly define our thermodynamic system. Assume that the small pump and the large pump initially have the knob pressed all the way down. So, initially, no air in the pumps.

Define our thermodynamic system to be the air initially in the container (at atmospheric pressure) plus the quantity of air initially in the atmosphere that will ultimately be pumped into the container using either four strokes of the small pump or one stroke of the large pump.

This system starts in an initial thermodynamic state, $i$, and ends in a final state, $f$. Clearly, the initial state of the system when using the small pump is the same as the initial state when using the large pump. Compare the final state of our system after 4 strokes of the small pump with the final state of the system after 1 stroke of the large pump. Are these final states the same? Justify your answer.

Use the first law of thermodynamics to relate the change in internal energy $\Delta U = U_f - U_i$, the work $W$ done on the system, and the heat $Q$ added to the system, as the system goes between initial and final states.

Can you see any way to proceed from here in order to eventually compare $W_1$ for the four strokes of the small pump with $W_2$ for the one stroke of the large pump? Hint: How is the change in entropy $\Delta S = S_f - S_i$ of the system related to the heat $Q$ and temperature $T$ for a reversible, isothermal process?

 

[Hak]

You do stroke 3 next. This would bedone by the same algorithm as was used for stroke 2. So, just mimic that.

Ok. I will report it in your exact words.

Stroke 3

In the first step of stroke 3, the gas is compressed until its pressure matches the pressure in the container that existed at the end of stroke 2, $$\displaystyle P_2=P_{atm}\frac{V_C+2V_p}{V_C}$$. By the end of this step, the volume in the pump has been reduced from $$\displaystyle V_p$$ to $$\displaystyle V_{3a}=V_p\frac{V_C}{(V_C+2V_p)}$$. So the work to compress the gas in step 3a is given by:

$$\displaystyle W_{3a}=P_{atm}V_p\ln{\frac{V_C}{(V_C+2V_p)}}$$

In the second step of stroke 3, the starting pressure is $$\displaystyle P_{atm}\frac{V_C+2V_p}{V_C}$$, the starting volume is $$\displaystyle V_C+V_p\frac{V_C}{(V_C+2V_p)}=V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)$$, and the final volume is $$\displaystyle V_C$$. So the work in second step of stroke 3 is:

$$\displaystyle W_{3b}=[P_{atm}\frac{V_C+2V_p}{V_C}][V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)]\ln{\frac{V_C}{V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)}}$$

$$\displaystyle W_{3b}=P_{atm}(V_C+3V_p)\ln{\frac{V_C+2V_p}{V_C+3V_p}}$$

The total work in stroke 3 is:

$$\displaystyle W_3 = W_{3a} + W_{3b}$$.

Is it correct?

 

[Hak]

Let's clearly define our thermodynamic system. Assume that the small pump and the large pump initially have the knob pressed all the way down. So, initially, no air in the pumps.

Define our thermodynamic system to be the air initially in the container (at atmospheric pressure) plus the quantity of air initially in the atmosphere that will ultimately be pumped into the container using either four strokes of the small pump or one stroke of the large pump.

This system starts in an initial thermodynamic state, $i$, and ends in a final state, $f$. Clearly, the initial state of the system when using the small pump is the same as the initial state when using the large pump. Compare the final state of our system after 4 strokes of the small pump with the final state of the system after 1 stroke of the large pump. Are these final states the same? Justify your answer.

Use the first law of thermodynamics to relate the change in internal energy $\Delta U = U_f - U_i$, the work $W$ done on the system, and the heat $Q$ added to the system, as the system goes between initial and final states.

Can you see any way to proceed from here in order to eventually compare $W_1$ for the four strokes of the small pump with $W_2$ for the one stroke of the large pump? Hint: How is the change in entropy $\Delta S = S_f - S_i$ of the system related to the heat $Q$ and temperature $T$ for a reversible, isothermal process?

Thank you very much. I'll try to think about it...

 

[Hak]

Let's clearly define our thermodynamic system. Assume that the small pump and the large pump initially have the knob pressed all the way down. So, initially, no air in the pumps.

Define our thermodynamic system to be the air initially in the container (at atmospheric pressure) plus the quantity of air initially in the atmosphere that will ultimately be pumped into the container using either four strokes of the small pump or one stroke of the large pump.

This system starts in an initial thermodynamic state, $i$, and ends in a final state, $f$. Clearly, the initial state of the system when using the small pump is the same as the initial state when using the large pump. Compare the final state of our system after 4 strokes of the small pump with the final state of the system after 1 stroke of the large pump. Are these final states the same? Justify your answer.

Use the first law of thermodynamics to relate the change in internal energy $\Delta U = U_f - U_i$, the work $W$ done on the system, and the heat $Q$ added to the system, as the system goes between initial and final states.

Can you see any way to proceed from here in order to eventually compare $W_1$ for the four strokes of the small pump with $W_2$ for the one stroke of the large pump? Hint: How is the change in entropy $\Delta S = S_f - S_i$ of the system related to the heat $Q$ and temperature $T$ for a reversible, isothermal process?

To compare the final state of the system after four strokes of the small pump with the final state of the system after one stroke of the large pump, I did the following assumptions:

1) The volume of the container, $\displaystyle V_C$, is constant and does not depend on the pump size or the number of strokes.
2) The volume of the pump, $\displaystyle V_P$, is proportional to the pump size, so the large pump has four times the volume of the small pump.
3) The pressure in the container, $\displaystyle P_C$, depends on the number of moles of gas in the container, $\displaystyle n_C$, and the temperature of the gas, $\displaystyle T$, according to the ideal gas law: $$\displaystyle P_C V_C = n_C R T$$.
4) The pressure in the pump, $\displaystyle P_P$, depends on the number of moles of gas in the pump, $\displaystyle n_P$, and the temperature of the gas, $\displaystyle T$, according to the ideal gas law: $\displaystyle P_P V_P = n_P R T$.
5) The temperature of the gas, $\displaystyle T$, is assumed to be constant and equal to the atmospheric temperature, $\displaystyle T_A$, since we are considering reversible isothermal processes.
6) The number of moles of gas in the container, $\displaystyle n_C$, increases by $\displaystyle n_P$ after each stroke, since one mole of gas is transferred from the pump to the container in each stroke.
7) The number of moles of gas in the pump, $\displaystyle n_P$, depends on the atmospheric pressure, $\displaystyle P_A$, and the volume of the pump, $\displaystyle V_P$, according to the ideal gas law: $\displaystyle n_P = \frac{P_A V_P}{R T_A}$.
Based on these factors, I calculated the final pressure in the container after four strokes of the small pump as:

$$\displaystyle P_{C,four} = \frac{n_{C,four} R T}{V_C} = \frac{(n_{C,i} + 4n_{P,s}) R T}{V_C} = \frac{(n_{C,i} + 4\frac{P_A V_{P,s}}{R T_A}) R T}{V_C} = P_{C,i} + 4\frac{P_A V_{P,s}}{V_C}$$

where $$\displaystyle n_{C,i}$$ is the initial number of moles in the container, $$\displaystyle n_{P,s}$$ is the number of moles in the small pump, and $$\displaystyle V_{P,s}$$ is the volume of the small pump.

Similarly, we can calculate the final pressure in the container after one stroke of the large pump as:

$$\displaystyle P_{C,one} = \frac{n_{C,one} R T}{V_C} = \frac{(n_{C,i} + n_{P,l}) R T}{V_C} = \frac{(n_{C,i} + \frac{P_A V_{P,l}}{R T_A}) R T}{V_C} = P_{C,i} + \frac{P_A V_{P,l}}{V_C}$$

where $$\displaystyle n_{P,l}$$ is the number of moles in the large pump, and $$\displaystyle V_{P,l}$$ is the volume of the large pump.

Since we know that $$\displaystyle V_{P,l} = 4V_{P,s}$$, we can see that:

$$\displaystyle P_{C,four} = P_{C,i} + 4\frac{P_A V_{P,s}}{V_C} = P_{C,i} + \frac{P_A (4V_{P,s})}{V_C} = P_{C,i} + \frac{P_A V_{P,l}}{V_C} = P_{C,one}$$

Therefore, I conclude that the final state of our system after four strokes of the small pump is exactly equal to that after one stroke of the large pump. This means that both processes have the same change in internal energy, $$\displaystyle \Delta U = U_f - U_i$$, and the same change in entropy, $$\displaystyle \Delta S = S_f - S_i$$, for our system.

In fact, the first law of thermodynamics states that:

$$\displaystyle \Delta U = Q + W$$

where $$\displaystyle Q$$ is the heat transferred to the system and $$\displaystyle W$$ is the work done on the system.

Since we know that $$\displaystyle \Delta U$$ is the same for both processes, we can write:

$$\displaystyle Q_{four} + W_{four} = Q_{one} + W_{one}$$

where the subscripts indicate the process of four strokes of the small pump or one stroke of the large pump.

The relation between entropy and heat for a reversible isothermal process states that:

$$\displaystyle Q = T \Delta S$$

where $$\displaystyle T$$ is the constant temperature of the system and $$\displaystyle \Delta S$$ is the change in entropy of the system.

Since we know that $$\displaystyle \Delta S$$ is the same for both processes, we can write:

$$\displaystyle Q_{four} = T \Delta S = Q_{one}$$

Substituting this into the previous equation, we get:

$$\displaystyle Q_{one} + W_{four} = Q_{one} + W_{one}$$

Simplifying, we get:

$$\displaystyle W_{four} = W_{one}$$

Therefore, I conclude that the work done on the system by four strokes of the small pump is exactly equal to that by one stroke of the large pump. This means that both processes have the same efficiency in transferring energy from the surroundings to the system.

Is that correct? Where am I going wrong?

Postscript. Sorry everyone, I misspelled the delivery of item 2.) The request is $W_1 - W_2$, not $W_2 - W_1$. Sorry again.

 

[TSny]

To compare the final state of the system after four strokes of the small pump with the final state of the system after one stroke of the large pump, I did the following assumptions:
...............

That all looks very good to me! Here's another way to see that the small pump and the large pump produce the same final thermodynamic state of the air in the container. Using four strokes of the small pump adds the same number of moles of air to the container as one stroke of the large pump. The temperature of the air and the volume of the container are assumed to remain constant. So, the final number of moles of air, the final air volume, and the air's final temperature will be the same for both pumps. The final states are the same for the two pumps since the thermodynamic state is determined by the number of moles, the volume, and the temperature.

I agree with your conclusion that the total work done by the four strokes of the small pump is equal to the work done by the one stroke of the large pump.

 

[Hak]

That all looks very good to me! Here's another way to see that the small pump and the large pump produce the same final thermodynamic state of the air in the container. Using four strokes of the small pump adds the same number of moles of air to the container as one stroke of the large pump. The temperature of the air and the volume of the container are assumed to remain constant. So, the final number of moles of air, the final air volume, and the air's final temperature will be the same for both pumps. The final states are the same for the two pumps since the thermodynamic state is determined by the number of moles, the volume, and the temperature.

I agree with your conclusion that the total work done by the four strokes of the small pump is equal to the work done by the one stroke of the large pump.

Ok, thanks, but... doesn't this mean that $W_1 - W_2 = 0$? If not, what is the work done by the one stroke of the large pump? How should I calculate it? Thanks.

 

[TSny]

Ok, thanks, but... doesn't this mean that $W_1 - W_2 = 0$?

Yes.

 

[Hak]

Yes.

Okay, now I'm curious if we get the same result with @Chestermiller's method....

 

[TSny]

Okay, now I'm curious if we get the same result with @Chestermiller's method....

Yes, I get the same result. It's interesting to work out the details and see that $W_1 = W_2$ according to @Chestermiller 's method.

 

[Hak]

Yes, I get the same result. It's interesting to work out the details and see that $W_1 = W_2$ according to @Chestermiller 's method.

So, is the following method correct?

Ok. I will report it in your exact words.

Stroke 3

In the first step of stroke 3, the gas is compressed until its pressure matches the pressure in the container that existed at the end of stroke 2, $$\displaystyle P_2=P_{atm}\frac{V_C+2V_p}{V_C}$$. By the end of this step, the volume in the pump has been reduced from $$\displaystyle V_p$$ to $$\displaystyle V_{3a}=V_p\frac{V_C}{(V_C+2V_p)}$$. So the work to compress the gas in step 3a is given by:

$$\displaystyle W_{3a}=P_{atm}V_p\ln{\frac{V_C}{(V_C+2V_p)}}$$

In the second step of stroke 3, the starting pressure is $$\displaystyle P_{atm}\frac{V_C+2V_p}{V_C}$$, the starting volume is $$\displaystyle V_C+V_p\frac{V_C}{(V_C+2V_p)}=V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)$$, and the final volume is $$\displaystyle V_C$$. So the work in second step of stroke 3 is:

$$\displaystyle W_{3b}=[P_{atm}\frac{V_C+2V_p}{V_C}][V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)]\ln{\frac{V_C}{V_C\left(\frac{V_C+3V_p}{V_C+2V_p}\right)}}$$

$$\displaystyle W_{3b}=P_{atm}(V_C+3V_p)\ln{\frac{V_C+2V_p}{V_C+3V_p}}$$

The total work in stroke 3 is:

$$\displaystyle W_3 = W_{3a} + W_{3b}$$.

Is it correct?

 

[TSny]

So, is the following method correct?

Yes, that looks good. But, note that your expressions for $W_{3a}$ and $W_{3b}$ will be negative quantities since the arguments of the logarithms are less than one. This has to do with Chestermiller's expressions that represent the work done by the air instead of the work done on the air. I believe the problem is asking for work done on the air by the person operating the pumps.

 

[Hak]

Yes, that looks good. But, note that your expressions for $W_{3a}$ and $W_{3b}$ will be negative quantities since the arguments of the logarithms are less than one. This has to do with Chestermiller's expressions that represent the work done by the air instead of the work done on the air. I believe the problem is asking for work done on the air by the person operating the pumps.

Ok, thank you. Is the method for finding stroke 4 the same?

 

[TSny]

Ok, thank you. Is the method for finding stroke 4 the same?

Yes.

 

[Hak]

Yes.

So $W_1$ is the sum of all 4 contributions, right? As for $W_2$? How should it be?

 

[TSny]

So $W_1$ is the sum of all 4 contributions, right?

Yes

As for $W_2$? How should it be?

That should be easy. It's very similar to the first stroke of the small pump.