Discussion Overview
The discussion focuses on estimating the reflecting color of a two thin-film system when illuminated by white light, particularly in the context of thin-film optics. Participants explore methods and approaches for calculating reflectance as a function of wavelength, considering the complexities of multi-layer systems.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant seeks guidance on estimating the reflecting color from a two thin-film system, indicating a lack of strong background in optics.
- Another participant suggests starting with the analysis for a single film to simplify the problem.
- A participant proposes obtaining reflectance as a function of wavelength using Fresnel equations and wave-transfer matrices, questioning the complexity of the approach.
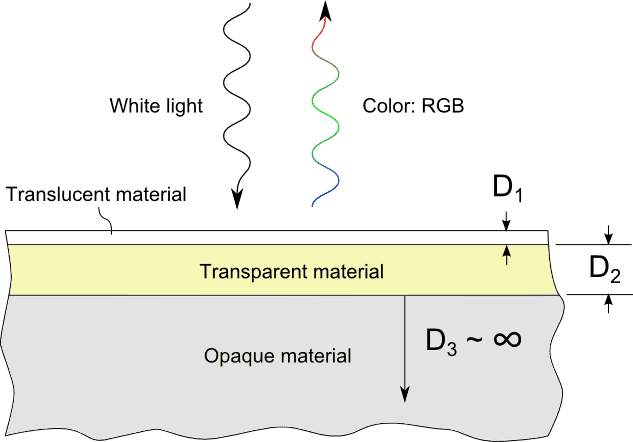
- Clarification is made regarding the term "translucent," with a participant indicating it refers to a layer that is between transparent and opaque.
- Discussion includes the need to calculate reflection and transmission at each boundary and the phase differences involved in multi-layer thin films.
- A participant shares a resource for an online reflectance calculator that uses the complex matrix form of the Fresnel equations.
- Concerns are raised about the complexity of the problem, with one participant initially unsure if it was a student exercise.
- Another participant describes a specific configuration of layers and suggests tuning thicknesses to achieve desired color removal through resonant transmission.
- A participant reports successfully implementing a method from a referenced source along with their own Python implementation.
Areas of Agreement / Disagreement
Participants express varying levels of understanding and approaches to the problem, with no consensus reached on a single method or solution. Some participants agree on the complexity of multi-layer systems while others propose different simplifications.
Contextual Notes
Participants mention missing specific information such as material properties and constants, which may affect the analysis. There is also uncertainty regarding the interpretation of terms and the overall complexity of the problem.
Who May Find This Useful
This discussion may be useful for individuals interested in thin-film optics, particularly those looking to understand the calculation of reflectance in multi-layer systems and the application of Fresnel equations.