Thought Experiment Proving Newtonian Momentum Not Conserved

[quasar987]

TL;DR

thought experiment proving momentum is not conserved

On p.170 of French's book on special relativity there is this thougth experiment attributed to Lewis and Tolman (1909). It is about two individuals throwing identical balls of mass M at each other with identical speed. The balls bounce against each other and are caught again.
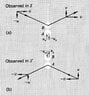
See attached picture. More precisely, individual B is on the enbankment and individual A is on the railway carriage. The relative motion is along the x-axis and the balls are thrown along the y axis. The Lorentz transformations imply that, according to A's frame, A's ball is thrown at velocity u=(0,u_y) but B's ball is thrown at velocity (v,-u_y/\gamma). The point of this thought experiment is that if the balls bounce back with the same (absolute) velocity that they were thrown, then Newtonian momentum is not conserved along the y axis:

$$Mu_y - Mu_y/\gamma \neq -Mu_y + Mu_y/\gamma$$

My question is simply this: why do we assume without a doubt that the balls bounce back with the same speed that they were thrown? If B's ball bounces back with speed (v,u_y) and A's ball bounces back with velocity (0,-u_y/\gamma) then Newtonian momentum is conserved.

 

[Halc]

So each ball has identical proper mass, and is propelled by say some kind of spring mechanism that imparts identical velocity to the ball in the rest frame of said mechanism. The two balls meet exactly halfway along the y axis.

In that case, the ball thrown from the rest frame (vertical) will have a higher speed (u) than the one it meets ($u/\gamma$), but the ball from the moving frame (diagonal) will have higher relativistic mass ($M*\gamma$), cancelling any difference in magnitude of momentum. Both balls should bounce back at the same speed it was thrown, preserving the symmetry of the situation, and conserving momentum as well.
Note that since the ball in a moving frame goes slower (y component at least), it must be thrown before the toss of the ball in the stationary frame.

 

[weirdoguy]

will have higher relativistic mass

I don't think it's a good idea to introduce relativistic mass since barely anyone uses it nowadays. Take a look at this insight:
https://www.physicsforums.com/insights/what-is-relativistic-mass-and-why-it-is-not-used-much/

 

[Ibix]

My question is simply this: why do we assume without a doubt that the balls bounce back with the same speed that they were thrown?

Start in an intermediate frame where the train and embankment have equal and opposite velocities and so do the balls. Trivially the pre- and post-collision velocities of each ball are equal except for a flipped sign on the y component, just from symmetry. This satisfies both relativistic and (accidentally) Newtonian momentum conservation. Then look at (or derive) the velocity transformation, in particular for components perpendicular to the frame velocity, and transform to S or S'. You'll find that it doesn't change the result about the y component of the velocity - and now you are at the beginning of your problem statement.

I don't have French to check, but does he not make some version of the argument above? If not, I completely understand your initial skepticism. Either way, collision problems are always easier in the Zero Momentum Frame , the frame where the net momentum of the colliding objects is zero. It's often a useful tool to think about that frame.

 

[quasar987]

Start in an intermediate frame where the train and embankment have equal and opposite velocities and so do the balls. Trivially the pre- and post-collision velocities of each ball are equal except for a flipped sign on the y component, just from symmetry. This satisfies both relativistic and (accidentally) Newtonian momentum conservation. Then look at (or derive) the velocity transformation, in particular for components perpendicular to the frame velocity, and transform to S or S'. You'll find that it doesn't change the result about the y component of the velocity - and now you are at the beginning of your problem statement.

I don't have French to check, but does he not make some version of the argument above? If not, I completely understand your initial skepticism. Either way, collision problems are always easier in the Zero Momentum Frame , the frame where the net momentum of the colliding objects is zero. It's often a useful tool to think about that frame.

Q.E.D.

 

[MathematicalPhysicist]

Good to see you @quasar987 you haven't been around the forums for sometime, or am I wrong?

 

[quasar987]

Good to see you @quasar987 you haven't been around the forums for sometime, or am I wrong?

Hi! You're right, it's been a very long while. I did a PhD in math and didn't have any time to think about physics, but now I'm back lol.