Time dilation and Einstein's theorem

[worlov]

I do not understand what the existence of the safe adds to the scenario.

I just wanted to emphasize that a clock works autonomously. Regardless of whether it is watched or not, a clock goes uniformly.

Einstein later tried to prove his „twin“ theorem with the general relativity:
https://en.wikisource.org/wiki/Translation:Dialog_about_Objections_against_the_Theory_of_Relativity

He modeled the acceleration phases with the imaginary gravitational field. Obviously, he relied on the principle of equivalence. However, the CERN researchers claim that the accelerations have no effect on the formula for time dilation of the special theory of relativity. So, this exchange – acceleration => gravitational field – is not justified. Moreover, the correctness of the principle of equivalence is also questionable. In this respect, Einstein's proof with the polygonal lines deserves more respect.

 

[Janus]

I just wanted to emphasize that a clock works autonomously. Regardless of whether it is watched or not, a clock goes uniformly.

Relativity does not require one to be watching the clocks. You are making the mistake that Relativity relies on the exchange of light signals, it doesn't. We use light in examples because it is convenient to illustrate the effects of Relativity, not because it is crucial to it. The only real reason that would require watching the clock would be to unsure that nothing other than it running at its normal rate happened during the course of the test ( it didn't stop running and start running again, a fault didn't cause it to start running fast, etc.)

Einstein later tried to prove his „twin“ theorem with the general relativity:
https://en.wikisource.org/wiki/Translation:Dialog_about_Objections_against_the_Theory_of_Relativity

He modeled the acceleration phases with the imaginary gravitational field. Obviously, he relied on the principle of equivalence. However, the CERN researchers claim that the accelerations have no effect on the formula for time dilation of the special theory of relativity. So, this exchange – acceleration => gravitational field – is not justified. Moreover, the correctness of the principle of equivalence is also questionable. In this respect, Einstein's proof with the polygonal lines deserves more respect.

The CERN test just verified the "clock postulate"; That when measured from an inertial frame, the rate at which a clock will tick is only effected by it velocity with respect to that frame and no additional effect is caused by any acceleration it may be undergoing.
But the equivalence principle deals with how the acceleration effects measurements made by the accelerating observer. CERN verified that particles accelerated do not show any additional time dilation as measured from the lab, but it did not measure how the accelerated particles measured the ticking of clocks in the lab.

 

[Herman Trivilino]

He modeled the acceleration phases with the imaginary gravitational field. Obviously, he relied on the principle of equivalence. However, the CERN researchers claim that the accelerations have no effect on the formula for time dilation of the special theory of relativity. So, this exchange – acceleration => gravitational field – is not justified. Moreover, the correctness of the principle of equivalence is also questionable. In this respect, Einstein's proof with the polygonal lines deserves more respect.

Many of the finest minds of the time used arguments far better than that to refute what Einstein had done, but since that time experiment and observation show that Einstein got it right. It is now an every day fact of life for thousands of scientists and engineers working all over the world.

 

[Dale]

CERN researchers claim that the accelerations have no effect on the formula for time dilation of the special theory of relativity. So, this exchange – acceleration => gravitational field – is not justified.

The equivalence principle is fully justified in many experiments and the results I believe you are referring to are fully consistent with relativity.

The problem is that people who have not worked through the math mistakenly believe that gravitational time dilation is related to gravitational acceleration, but it is actually related to gravitational potential. So the fact that accelerations have no effect is predicted by both, and what has the effect is the potential whether it is the gravitational potential or the inertial potential that arises in an equivalent accelerating reference frame.

The mathematical concept that Einstein used to model the artificial gravitational field is called Christoffel symbols. The relationship is completely rigorous, even though it is not a large focus of relativity in practice. But he is fully justified in his description in that paper.

 

[Ibix]

Here are some spacetime diagrams to explain why the time dilation formulae don't work here, and why the relativity of simultaneity is important. I've done this for a simple out-and-back twin paradox with instantaneous turnaround and a constant velocity of 0.6c. The extension to more complicated cases is messy, but fundamentally the same.

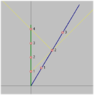
First, here's a spacetime diagram of the stay-at-home clock (blue worldline) and the traveling clock (red worldline) in the frame of the stay-at-home:

The turnaround happens at time $T$. But now let's think about the outbound frame, the frame in which the traveling clock is at rest as it travels to the right. The turnaround happens at time $T'=T/\gamma$ in this frame. But the Lorentz transforms tell us that $T'=\gamma(t-vx/c^2)$, which is to say that "at the same time as the turnaround according to the outbound frame" is a sloped line on this graph, satisfying $t=T'/\gamma+vx/c^2=T/\gamma^2+vx/c^2$. That's the dashed line in the diagram below:

The dashed line intercepts the stay-at-home clock's (blue) worldline at $t=T/\gamma^2$. This is exactly consistent with time dilation - the traveling clock experiences $T/\gamma$ of elapsed time, and measures $1/\gamma$ less time on the stay-at-home clock.

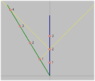
Now let's turn our attention to the inbound frame. The maths here is a bit messier. The turnaround in this frame happens at $T''=\gamma(1+v^2/c^2)T$. Again, the Lorentz transforms tell us that $T''=\gamma(t+vx/c^2)$, or $t=(2T-T/\gamma^2)-vx/c^2$. Again, this is a sloped line, but it is not the same sloped line as above - it slopes in the opposite direction.

Again, this is consistent with the time dilation formula. The traveling clock experiences time $T/\gamma$ on the inbound leg, and measures the stay-at-home clock to experience less time by another factor of $1/\gamma$.

But now we can see what's gone wrong. The time up to $T/\gamma^2$ on the stay-at-home clock is "during the outbound leg" according to the outbound frame, and the time after $2T-T/\gamma^2$ is "during the inbound leg" according to the inbound frame. But because we changed our definition of "at the same time as the turnaround", to naively apply the time dilation formula is to forget about the middle portion of the worldline. This is why there is no problem with the behaviour of the stay-at-home clock - it ticks 2T times. But if you don't account for the relativity of simultaneity you have forgotten about $2Tv^2/c^2$ of them.

 

[Grimble]

But the Lorentz transforms tell us that T′=γ(t−vx/c2)

but surely x - the distance the clock has travelled, OD, = vt
then
T'=γt(1-v²/c²) = t/γ

in the frame of the stay-at-home:

. The distance OT' is the distance, if the traveling clock were a light clock, that light would have traveled from the initial event O to the red turnaround at time T' in the stay-at-home frame.
... and T' occurs at time T on the time axis on the stay-at-home clock's frame
One cannot get much more basic than time and distance axes, T and X at 90°.

I am sorry but I am just having difficulty following what is wrong with the most simple and basic mathematical principles - or maybe I am just being naïve... ?

 

[Janus]

but surely x - the distance the clock has travelled, OD, = vt
then
T'=γt(1-v²/c²) = t/γ

. The distance OT' is the distance, if the traveling clock were a light clock, that light would have traveled from the initial event O to the red turnaround at time T' in the stay-at-home frame.
... and T' occurs at time T on the time axis on the stay-at-home clock's frame
One cannot get much more basic than time and distance axes, T and X at 90°.

I am sorry but I am just having difficulty following what is wrong with the most simple and basic mathematical principles - or maybe I am just being naïve... ?

To do a light clock analysis using the space-time diagram, you would have to add another axis, y (coming straight out of the screen) to represent the distance between the mirrors which is perpendicular to the relative motion of the clocks. As drawn the time-space diagram only deals with the time axis and the axis along the relative velocity of the clocks.

And while T and X axis at 90 degrees is basic, and both frames measure T and X at being 90 degrees, They don't measure T and X along the same axis.

Start with two clocks A and B, which start at the same point, both reading 0, and separate at 0.6c. When Clock A reads 1 it sends a light signal to B and B then sends it back.
In the frame of A (green world line), the space-time diagram looks likes this.

The light (yellow line), arrives at B when it reads 2 and returns when A reads B. the light lines are drawn at 45 degree angles, as that is the time to space scale of the diagram. According to A, the light leaves some time before B reads 1 and returns a bit after B reads 3. B also ticks off it time at a slower rate.

From the frame of B (blue line), events unfold like this:

The light still leaves A when it reads 1, arrives at B when it reads 2 and returns to A when A reads 4. To maintain a invariant speed for light the light lines must still be drawn at 45 degree angles. To keep this consistent with the departure and arrival readings, the light leaves A after clock B reads 1 and returns to A well after B reads 3 ( it looks like a bit after B reads 5)

The time and space axis are not fixed features of space-time, but are frame dependent.

 

[Ibix]

but surely x - the distance the clock has travelled, OD, = vt
then
T'=γt(1-v²/c²) = t/γ

But here you are telling me the time $t$ on a clock instantaneously colocated with the ship when the ship's clock reads $T'$. I'm telling you what a clock at any $x$ reads when it's instantaneously colocated with a moving clock (moving at the same speed as the ship, but not necessarily in the same place) reads $T'$.

The distance OT' is the distance, if the traveling clock were a light clock, that light would have traveled from the initial event O to the red turnaround at time T' in the stay-at-home frame.

This sentence is somewhat tortured, but I think it's correct.

One cannot get much more basic than time and distance axes, T and X at 90°.

As drawn on a Minkowski diagram, if the $x$ and $t$ axes are at right angles then $x'$ and $t'$ axes are not. They are orthogonal in Minkowski geometry, but the screen obeys Euclidean geometry so I can't draw things that obey Minkowski geometry accurately.

 

[sweet springs]

Each observer determines that all clocks in motion relative to that observer run slower than that observer’s own clock.

Not so. Say a space pilot gets on a large turn table of radius R and turning speed R $\omega$ and make a cosmic round trip and get it off and return to the Earth.
The pilot is in round motion for the Earth. The pilot clock has ticked slower when they meet.
The Earth is in round motion for the pilot. However, the pilot clock has ticked slower when they meet.

 

[jbriggs444]

Not so. Say a space pilot gets on a large turn table of radius R and turning speed R $\omega$ and make a cosmic round trip and get it off and return to the Earth.
The pilot is in round motion for the Earth. The pilot clock has ticked slower when they meet.
The Earth is in round motion for the pilot. However, the pilot clock has ticked slower when they meet.

It is far from clear what measurements you are describing here. The unambiguous fact of the matter is that the clock held by the rotating pilot will be seen to have ticked fewer times when the clocks are reunited. This in no way contradicts the legitimacy of a series of tangent frames in which each clock ticked more slowly than the other throughout the scenario.

However, time dilation is indeed not the whole story. When hopping from tangent frame to tangent frame to build a global picture of the situation, relativity of simultaneity is an important concept to grasp.

 

[sweet springs]

When hopping from tangent frame to tangent frame to build a global picture of the situation, relativity of simultaneity is an important concept to grasp.

Go-return rocket experiences only one hopping when turning around. Turning round trip pilot does continuous and homogeneous hoppings in tangent IFRs. Accumulated time dilation results when meeting again are same ratio of $\sqrt{1-v^2/c^2}$.　It applies for any closed trajectory in the Earth's IFR with tangent speed v.　

Rotating frame of reference which is interpreted as integrated tangent IFRs gives up synchronization of clocks as well as simultaneity. Absolute past and future are important but simultaneity depends on frames of reference and not defined in some frames. Should we rely on concept of simultaneity to the end ?

 

[sweet springs]

Each observer determines that all clocks in motion relative to that observer run slower than that observer’s own clock. If the moving observer returns to point A, he will notice the following: the clock at point A is slower than his own clock. but this clock shows that more time has passed since his departure than his own clock. For moving observers this conjucture makes no sense. If a clock is slower than its own clock, it should also show less time. Therefore, the clock in point A should be synchronized according to the rules of relativity ... but how?

In scenario of go-return rocket, we have three IFRs of A, say the Earth, go rocket and return rocket.

Say as for coordinate settings, the Earth IFR and go rocket IFR have coordinate time zero and space zero for the departure event, and go rocket IFR and return rocket IFR have coordinate of same time and same space for the turning event.

As for meeting again event, the three IFRs' networked clocks superposed on the Earth show different ticks. Readings of three superposed IFR clocks on the meeting again event are

return rocket < the Earth < go rocket

Each of three clock is synchronized in each IFR's clock network. Though each criticizes other two clocks for wrong synchronization, you do not have to worry about it. Synchronization is relative.

PS
For another setting, say all three IFRs have coordinate of time zero and space zero for the departure event, the readings of three superposed clocks at the event of meeting again are

the Earth < go rocket = return rocket

Say T the difference of go rocket IFR clock and return rocket IFR clock at the event of turning. Go rocket IFR clock is delayed much with relative speed $\frac{2v}{1+v^2/c^2}\approx 2v$ for return rocket IFR clock. By draw back of T in the return rocket clock

return rocket - T < the Earth < go rocket

This is same as the original setting above.

 

[Grimble]

But here you are telling me the time tt on a clock instantaneously colocated with the ship when the ship's clock reads T′T'. I'm telling you what a clock at any xx reads when it's instantaneously colocated with a moving clock (moving at the same speed as the ship, but not necessarily in the same place) reads T′T'.

You have lost me here... - what I am saying is that the distance the traveller (on his spaceship) has traversed is the velocity he is traveling at x the time he has traveled - x=vt - (pretty basic mechanics surely) and that that substituted into the Lorentz time equation ...

 

[Ibix]

You have lost me here... - what I am saying is that the distance the traveller (on his spaceship) has traversed is the velocity he is traveling at x the time he has traveled - x=vt - (pretty basic mechanics surely) and that that substituted into the Lorentz time equation ...

$x$ is where something is, not the distance it's travelled. However, the ship started at $x=0$, so in the specific case of the ship $x$ is equal to the distance travelled. For other clocks moving at the same speed as the ship but not at the same place, $x\neq vt$.

 

[Grimble]

But what 'other clocks' ?
The traveling clock is on board the spaceship. That is what this is all about - what have other clocks to do with it?

 

[jbriggs444]

But what 'other clocks' ?
The traveling clock is on board the spaceship. That is what this is all about - what have other clocks to do with it?

If there is a "travelling" clock, there is a frame in which it is travelling. In that frame, it makes sense to speak of x=vt. However, the clock that measures that t is not the traveling clock.

There is also a frame in which the traveling clock is at rest. The traveling clock measures time too, of course. But in its rest frame, v=0 and x=0.

 

[Ibix]

But what 'other clocks' ?
The traveling clock is on board the spaceship. That is what this is all about - what have other clocks to do with it?

The point is that "at the same time as the ship turns around, back on Earth" means different things to different frames. So the interesting question is: when a clock at rest in the outbound ship frame passes the Earth showing the same time as the ship clock shows at turnaround, what time is it according to the Earth's clocks? And similarly for the inbound frame.

 

[Grimble]

Yes, of course, but in the frame of that clock it is at rest, not travelling.
It is, and can only be (in this thought experiment) ... only be traveling in the resting frame of clock T.
So how can v=0, x=0 in the Lorentz equation for a traveling clock? - that just seems to make no sense ...

 

[Grimble]

I'm sorry but we seem to be missing something here - Einstein's first postulate.

Let us look at this in its simplest view.
We have two frames, two inertial frames, in each of which there is a stationary clock. To an observer in frame A clock A is at rest and clock B, at rest in frame B , moving at v relative to A.
Two identical clocks in inertial frames.
Let us suppose they are light clocks.
When the light in clock A has traveled 1 light second to its mirror, it will measure 1 second to have passed and clock A will display (read) 1 second.
When the light in clock B has traveled 1 light second to its mirror, it will measure 1 second to have passed and will display (read) 1 second.
Frame A and Frame B are inertial frames and all we are measuring is how long it takes for light to travel 1 light second in each frame. the same time - 1 second measured from O when the clocks were co-located.
I am not saying that this is simultaneous because that judgement depends on the convention for simultaneity chosen; but I will say that they both happen at the end of equal intervals measured from event O.
Both clocks will read the same at turnround.
However, I am not saying that the traveling clock is not slow - it certainly is - but compared to what? Surely oit must be compared to A's measurement of the turnround time of T' that is the turnround time of B, in A's frame in which the light in clock B has traveled 1 light second to its mirror AND the distance that clock has traveled from clock A.
That is it will have travelledthe distance OT' or γT.

 

[Dale]

I'm sorry but we seem to be missing something here - Einstein's first postulate.

If you are using the Lorentz transform then you are not missing either of Einstein’s postulates. Both postulates are built into the Lorentz transform.

 

[stevendaryl]

I'm sorry but we seem to be missing something here - Einstein's first postulate.

Let us look at this in its simplest view.
We have two frames, two inertial frames, in each of which there is a stationary clock. To an observer in frame A clock A is at rest and clock B, at rest in frame B , moving at v relative to A.
Two identical clocks in inertial frames.
Let us suppose they are light clocks.
When the light in clock A has traveled 1 light second to its mirror, it will measure 1 second to have passed and clock A will display (read) 1 second.
When the light in clock B has traveled 1 light second to its mirror, it will measure 1 second to have passed and will display (read) 1 second.
Frame A and Frame B are inertial frames and all we are measuring is how long it takes for light to travel 1 light second in each frame. the same time - 1 second measured from O when the clocks were co-located.
I am not saying that this is simultaneous because that judgement depends on the convention for simultaneity chosen; but I will say that they both happen at the end of equal intervals measured from event O.
Both clocks will read the same at turnround.
However, I am not saying that the traveling clock is not slow - it certainly is - but compared to what? Surely oit must be compared to A's measurement of the turnround time of T' that is the turnround time of B, in A's frame in which the light in clock B has traveled 1 light second to its mirror AND the distance that clock has traveled from clock A.
That is it will have travelledthe distance OT' or γT.

I would sort of like to help out, but I don't quite understand what is at issue. You have two rest frames A and B, and there are clocks at rest in each frame. So what exactly is the issue or question?

 

[Ibix]

@Grimble - as @Dale notes, I explicitly use the Lorentz transforms which are derived from the two postulates. So no, I am not forgetting the first postulate.

Let's try this another way. The question is: what time is it on Earth when the rocket turns around?

In the Earth frame the answer is trivial - the rocket turns around at time $T$ because that's how we defined the experiment.

In the ship frame it's also trivial - it's $T/\gamma$, which I called $T'$, because that's what the ship's clock reads at turnaround.

But what are we to make of the fact that the frames disagree about the time of turnaround? What do Earth clocks show? Do they show $T$ or $T'$ or something else? The OP in this thread was trying to argue that this confusion proved that there was some kind of absolute time, I think. But he forgot about the relativity of simultaneity.

In the ship frame, the Earth is doing $-v$. So at the same time as the ship turns round its coordinates are $x'=-vT'$, $t'=T'$. You can use the inverse Lorentz transforms to determine what an Earth frame clock reads at this event, which is $T/\gamma^2$. And this is the point: "on Earth at the same time (as defined by the ship frame) as the turnaround" is an event a lot earlier on the Earth's worldline than "on Earth at the same time (as defined by the Earth frame) as the turnaround".

The slanted grey line in my Minkowski diagram connects all events that are "at the same time (as defined by the ship frame) as the turnaround". A horizontal line would connect all events that are "at the same time (as defined by the Earth frame) as the turnaround". They are different because simultaneity is relative. What "now" means depends on where you are and which frame you are using.

 

[Grimble]

All I am using is Newtonian mechanics PLUS Einstein's two postulates.
Those postulates tell us that the time for light to travel the distance OT in clock A in frame A, is equal to the time it takes light to travel the distance DT' in clock B in frame B.
Equal times for light to travel equal distances in inertial frames.
Simple mechanics...

 

[jbriggs444]

All I am using is Newtonian mechanics PLUS Einstein's two postulates.
Those postulates tell us that the time for light to travel the distance OT in clock A in frame A, is equal to the time it takes light to travel the distance DT' in clock B in frame B.
Equal times for light to travel equal distances in inertial frames.
Simple mechanics...

Careful definition of terms would help. And a careful explanation of the point you are trying to reason toward.

Here, "O" denotes the event where the the near mirrors of the A and B light clocks are co-located and simultaneously started?

And, "T" denotes the event where light in A's light clock reaches its far mirror for the first half-tick?

And "T'" denotes the event where light in B's light clock reaches its far mirror for the first half-tick?

If so, what in the heck is D?

 

[Dale]

All I am using is Newtonian mechanics PLUS Einstein's two postulates.

Newtonian mechanics is incompatible with Einstein’s second postulate.

 

[jbriggs444]

Newtonian mechanics is incompatible with Einstein’s second postulate.

I suspect (or hope) that @Grimble is only borrowing from Newtonian mechanics the notions of Euclidean 3-space and of inertial frames. In particular that, within a given inertial frame, an object subject to no external forces has constant velocity and a position function of the form $\vec x=\vec{x_0} + \vec{v}t$.

 

[Ibix]

If so, what in the heck is D?

I believe @Grimble is referencing my Minkowski diagrams from post #35. But I share your confusion over whether he is using the letters to reference events or places/times. Neither interpretation seems consistent with what he is writing at the moment.

 

[SiennaTheGr8]

Often it seems that beginners think they understand the relativity of simultaneity but actually do not. This is one reason I like David Morin's approach, which introduces the "rear clock ahead" principle early on. See also the "Andromeda Paradox," or this thought-provoking version of it (courtesy of Don Koks).

 

[Herman Trivilino]

All I am using is Newtonian mechanics PLUS Einstein's two postulates.

But that's not the way the physics works. The consequences of Einstein's postulates don't agree with Newtonian mechanics.