Discussion Overview
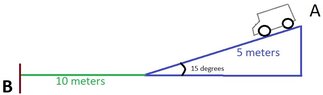
The discussion revolves around calculating the time it takes for a 2000 kg truck to travel down a 15-degree ramp and reach point B. The problem involves concepts of physics such as acceleration, forces acting on the truck, and kinematics, while assuming no air resistance and a coefficient of kinetic friction.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
Main Points Raised
- One participant presents the problem of a truck on a ramp and seeks to determine the time taken to travel from point A to B.
- Another participant suggests that the original post is incomplete and directs attention to an external link for a similar problem, implying that it may provide useful insights.
- A subsequent reply notes that the external link requires a paid membership and does not specifically address the time calculation from A to B.
- Further suggestions include using Google to find additional resources on the equations related to acceleration down a ramp.
- One participant provides a detailed breakdown of the physics involved, referencing Newton's second law and kinematics equations, while outlining the steps needed to calculate both the acceleration down the ramp and the time taken on the horizontal surface.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the solution to the problem, and multiple approaches and resources are suggested without agreement on a definitive method or answer.
Contextual Notes
The discussion lacks specific numerical values for the displacement down the ramp and the speed at the ramp bottom, which are necessary for complete calculations. Additionally, the assumptions regarding air resistance and friction are acknowledged but not elaborated upon.