Time it takes a 3-body gravitational system to complete one orbit?

[UTlonghorn]

Homework Statement

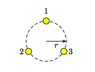
There is no general analytical solution for the motion of a three-body gravitational system. However, there do exist analytical solutions for very special initial conditions. The figure below (see attachment) shows three stars, each of mass m, which move in a two-dimensional plane along a circle of radius r. Calculate how long this system takes to make one complete revolution. (In many cases, three-body orbits are not stable: any slight perturbation leads to a breakup of the orbit.)

Homework Equations

This course focuses heavily on the Momentum Principle.

mv²/R=GMm/R²

v=(GM/R)^1/2

v=(2(pi)R)/T

(2(pi)R)/T=(GM/R)^1/2 where T is the time it takes to complete one complete revolution.

The Attempt at a Solution

I thought you could just replace Mm with m³ since the stars all have equal mass and then solve for T, but it's not in the answer choices. The answer is one of the choices in the attachment.

 

[gneill]

You'll need to work out the net gravitational force that anyone of the stars feels from the other two. By symmetry this should be directed towards the center of the circle.

What sort of triangle do the stars form, if the stars are at the vertexes?

 

[UTexasEng]

I have this same problem too. The three bodies are arranged in an equilateral triangle, and each of them lay on a point of the radius of the circle.

Update: My bad, I thought you could not see the attached pictures.

 

[gneill]

The same advice as before applies. Find an expression for the net gravitational force on any given body due to the other two. That net force provides the centripetal force required to move the body in circular motion...