Time taken by a balloon to deflate

[Saitama]

Homework Statement

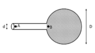
A soap bubble is blown with a relatively short drinking straw of diameter d, and then the bubble is left to deflate through the same straw. In one case when the diameter of the bubble was D the time during which the bubble deflated was 8 seconds. Estimate the time during which a bubble deflates

a) if its diameter is also D, and it is deflated through a wider straw of diameter 2d;

b) through a straw of diameter d, if its greatest diameter was 2D?

Homework Equations

The Attempt at a Solution

The air inside the bubble moves out because of the pressure difference between the two ends of straw. The pressure difference is $4T/r$, where $T$ is the surface tension of soap liquid and $r$ is the radius of bubble at any time. I feel I have to find the time ($dt$) in which the radius of bubble decreases by $dr$ and then integrate it but how do I find an expression for $dt$?

Any help is appreciated. Thanks!

 

[TSny]

The escaping air is a fluid in motion. There's some sort of principle that applies to such things.

 

[Saitama]

The escaping air is a fluid in motion. There's some sort of principle that applies to such things.

Bernoulli? :D

But I am not sure at which two points I should apply it. Should the two points be the two ends of the straw?

 

[TSny]

Bernoulli's principle applies to points along the same streamline. It might be good to consider a streamline that "starts" well inside the bubble and extends through the straw.

 

[Saitama]

Bernoulli's principle applies to points along the same streamline. It might be good to consider a streamline that "starts" well inside the bubble and extends through the straw.

Do you mean points A and B?

 

[TSny]

Yes and no.

 

[Saitama]

Yes and no.

Sorry TSny but I don't get it.

 

[PhysicoRaj]

Yes for point 'A' and no for 'B'. I think this was what TSny was telling.

 

[I like Serena]

Hey Pranav!

I do not know what TSny and PhysicoRaj mean with those points A and B.
They seem fine to me.

Also, I see no way to apply Bernoulli here.
It doesn't say much on how the flow changes over time.

I would use that the rate at which air goes through the straw is linear with the pressure difference on both ends.
And also linear with the area of a cross section of the straw.
In other words:
$$\frac{dV}{dt} = k \cdot \Delta p \cdot d^2$$
for some constant $k$.

 

[TSny]

By using Bernoulli, I get an equation something like I_Like_Serena's, but with the rate of change of volume not proportional to the pressure difference. (But I could be wrong, of course. )

The reason point B isn't of much help is that it's right at the entrance to the straw where the air will certainly be in motion and the pressure is unknown. Why not extend the streamline farther back into the interior of the bubble where you should be able to approximate both the speed and pressure?

[EDIT: Bernoulli or Poiseuille or what? Key words to me are "relatively short" and "drinking straw".]

 

[I like Serena]

Wiki says about Poiseuille:
"The assumptions of the equation are that the fluid is incompressible and Newtonian",
although there is and adjusted version for compressible fluids.

Wiki also says:
"The equation fails in the limit of low viscosity, wide and/or short pipe."
I think that is applicable here.


As for Bernoulli, under the circumstances described we would have:
$$\frac{p_B}{\rho_B} = \frac{p_o}{\rho_o} + \frac{v_o^2}{2}$$
where $v_o$ is the speed at the outlet.

Since air is close to a perfect gas, we also have:
$$\frac{p}{\rho} = \frac{RT}{M}$$
where $M$ is the molar mass.

Either way, I do not see how this tells us much about the volumetric flow.

 

[TSny]

I think we can treat the air flow as approximately incompressible in this problem. The difference in pressure between inside and outside of a typical soap bubble is of the order of 1 ~ 10 N/m². This is very small compared to the atmospheric pressure itself. So, the percent change in pressure of the air as it escapes is very small.

If you can estimate the speed of the air at point A, then you can estimate the rate at which the volume is decreasing.

 

[Saitama]

I tried Poiseuille law but I don't seem to be getting the right answer.

Poiseuille law states that:
$$\frac{dV}{dt}=k\cdot \Delta p\cdot d^4$$
In our case,
$$\frac{dV}{dt}=-4\pi r^2\frac{dr}{dt}$$
$$\Delta p=\frac{4T}{r}$$
Plugging the above in the D.E
$$-4\pi r^2\frac{dr}{dt}=\frac{4Tkd^4}{r}$$
Integrating gives
$$t\propto \frac{D^4}{d^4}$$
For the first part of problem I get t=0.5 seconds which is incorrect. :(

The correct answer is about 2 seconds.

 

[I like Serena]

As stated, Poiseuille's law does not apply. It requires significant viscosity and a long pipe.

 

[I like Serena]

Wiki says:
"If the pipe is too short, the Hagen–Poiseuille equation may result in unphysically high flow rates."

In other words, the volumetric rate is not correlated to $d^{4}$.

 

[haruspex]

Ua

The correct answer is about 2 seconds.

If you use the equation in post #9 I think you get that answer.

 

[Chestermiller]

Bernoulli's equation gives:
\frac{1}{2}ρv^2=\frac{8σ}{D}
where σ is the surface tension.
The mass discharge rate of air from the bubble through the straw is π\frac{d^2}{4}ρv. For our purposes, the density of the air inside the bubble is not significantly different from that of the surrounding air at 1 atm. So,
\frac{πρ}{6}\frac{dD^3}{dt}=-π\frac{d^2}{4}ρv
Just combine the equations by eliminating v.

Chet

 

[Saitama]

Bernoulli's equation gives:
\frac{1}{2}ρv^2=\frac{8σ}{D}
where σ is the surface tension.
The mass discharge rate of air from the bubble through the straw is π\frac{d^2}{4}ρv. For our purposes, the density of the air inside the bubble is not significantly different from that of the surrounding air at 1 atm. So,
\frac{πρ}{6}\frac{dD^3}{dt}=-π\frac{d^2}{4}ρv
Just combine the equations by eliminating v.

Chet

Thanks Chestermiller, I get the right answer using your equations. :)

Solving the D.E gives:
$$t \propto \frac{D^{7/2}}{d^2}$$
For the first part, I get $t=2\,\,\text{seconds}$ and for the second part, I get $t=64\sqrt{2}\,\,\text{seconds}$ and both are correct.

Thanks a lot TSny, ILS and Chestermiller.