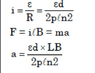To find the Acceleration of a Pentagonal metallic plate

[Amitkumarr]

Homework Statement

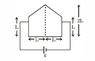
A metallic plate is of the shape of an pentagon. Its thickness is d. It is kept in a uniform magnetic field B perpendicular to the plate as shown. The ends of the plate are connected to a battery of emf ɛ. If the density of the material of the plate is r, find its acceleration (in m/s^2). The surface on which plate rests is smooth and connecting wires do not exert any force on the plate. The battery is ideal. Resistivity of material is p. Take B =0.77 T, ɛ = 2.7 V, p = 10^-3 ohm m, r = 2 x 10^3
kg/m^3, D = 1 mm, L = 1 m. [Take : ln2 = 0.693]

Relevant Equations

Current, I=ɛ/R
where ɛ= E.M.F of the cell,R= Resistance
R=pL/A where p=Resistivity of the material,l=length,A=Area
Force,F=ILB=ma where B=Magnetic field
a=Acceleration

In order to find force( and hence the Acceleration) on the Pentagonal plate,we must find the Resistance of the plate.But to find the resistance we must know how the current is flowing through the given plate(see attached figure).

My question is how is the current flowing through the Pentagonal plates and further how to proceed to find resistance?According to me,we should be using integration,if so how to take the elements?

 

[TSny]

My question is how is the current flowing through the Pentagonal plates and further how to proceed to find resistance?According to me,we should be using integration,if so how to take the elements?

That's a good question. The pattern of current would certainly be complicated. So, it will not be possible to calculate the actual effective resistance. However, as an academic exercise, you are probably meant to assume a simplification where you break the plate into infinitesimal strips and assume that the current is uniform through each strip.

So, you need to think about how to choose the strips. Integration is a summation. You know that resistances in series add.

 

[Amitkumarr]

That's a good question. The pattern of current would certainly be complicated. So, it will not be possible to calculate the actual effective resistance. However, as an academic exercise, you are probably meant to assume a simplification where you break the plate into infinitesimal strips and assume that the current is uniform through each strip.

So, you need to think about how to choose the strips. Integration is a summation. You know that resistances in series add.

If we take vertical strips( like in the attached figure d=width of plates), resistance for first half part of the Pentagonal plate comes out be R1=(p×ln2)/d and same for the second half part.
So,total resistance,R=2×R1= 2×(p×ln2)/d

But,how do we find the force on the plate using the general expression for a current carrying conductor,F=ILB ?What about forces on the upper triangular portion of the pentagon?
I just found that in my solution manual(see attached figure),they have calculated Net force as F=I×L×B=(ɛ÷R)×L×B where R is same as calculated above.How they have done so?

 

[TSny]

But,how do we find the force on the plate using the general expression for a current carrying conductor,F=ILB ?What about forces on the upper triangular portion of the pentagon?
I just found that in my solution manual(see attached figure),they have calculated Net force as F=I×L×B=(ɛ÷R)×L×B where R is same as calculated above.How they have done so?

Consider the force dF on one of the vertical strips. Assume the current through the strip is horizontal. Write an expression for dF.

 

[Amitkumarr]

Consider the force dF on one of the vertical strips. Assume the current through the strip is horizontal. Write an expression for dF.

One clarification,we are assuming magnetic field to be perpendicular to plates and in the plane of Pentagonal plate and not perpendicular to it's plane,right?If, we consider the current through the strip to be horizontal,we will have to take length of strip as x+L because L and B needs to be perpendicular to each other(in the F=ILB expression) and magnetic field is given parallel to the plates i.e Perpendicular to strip and in the plane of strip.So, the expression should become dF=I×(x+L)×B . Then,how will we proceed?
Could you please write the complete expression?

 

[TSny]

I think B is perpendicular to the plane of the pentagon.

 

[Amitkumarr]

Thanks,I finally realized that the solution given was wrong as it takes different values of B and p. The correct expression for force will be F=(ɛdlB)÷pln2 and so the correct answer is a=1 m/s^2.