To get rid of a singularity in the Lagrange equations

[wrobel]

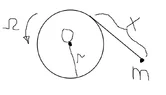
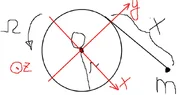
A disk of radius $r$ is wrapped with an inextensible massless string. A particle of mass $m$ is attached to the end of the string. The disk rotates about its center $O$ with angular velocity $\Omega=const$. The whole system is placed on a smooth horizontal table.
This is a Lagrangian system with one degree of freedom. To study this system take $x,\quad x>0$ the length of the free tail of the string as a generalized coordinate.
It is easy to calculate the Lagrangian
$$L=\frac{1}{2}\frac{m}{r^2}x^2\dot x^2+\frac{1}{2}m\Omega^2x^2.$$
The Lagrange equation has a singularity at $x=0$ . To get rid of this problem introduce a new variable $\xi=x^2.$ The Lagrangian takes the form
$$L=\frac{1}{8}\frac{m}{r^2}\dot \xi^2+\frac{1}{2}m\Omega^2\xi.$$
To understand the dynamics it is convenient to draw a phase portrait that is to draw a set of level lines of the generalized energy integral $$H=\frac{1}{8}\frac{m}{r^2}\dot \xi^2-\frac{1}{2}m\Omega^2\xi$$ in the plane $(\xi,\dot \xi)$.
It is interesting to note that the system has solutions that first wind up on the coil and then wind off the coil; the particle does not touch the coil.
Also there are solutions $x(t)$ such that $\dot x\to-\infty$ as $x\to 0$.

 

[anuttarasammyak]

Does the wire wrapping direction wrt $\Omega$ matter in your result ? It seems that one tighten and the other loosen the wire.

 

[wrobel]

For intuition it is convenient to consider the wrapping direction as it is shown at the picture and to assume that the string remains tighten. I have written formulas in such an assumption. Anyway all these words just describe an ideal constraint we use.

 

[anuttarasammyak]

I see.

Tension from the wire (blue) generates centripetal force (green) for circulation of m. The rest component (purple) causes unwrapping the wire. Thus x increases with time.

Am I correct ?

 

[wrobel]

it seems yes

 

[anuttarasammyak]

Thanks.　
For x/r $\rightarrow \infty$, the purple force decreases so $\dot{x}$ would also decrease.
For x=0 wire tension cannot generate centripetal force. The singularity would come from it.
For x=+0 wire tension is +$\infty$ thus the purple force is also +$\infty$ which would cause infinite $\dot{x}$.

 

[wrobel]

Actually we do not know how the centripetal force is directed. To understand that one must know the trajectory first.

 

[anuttarasammyak]

I try to make the Lagrangian. Say coordinate of m is (X,Y)
$$X=r \sec \phi \ \cos (\theta - \phi) $$
$$Y=r \sec \phi \ \ sin (\theta - \phi) $$
where
$$\theta = \Omega t + \frac{x}{r} + \theta_0-\frac{x_0}{r} $$
$$\phi = \tan^{-1}\frac{x}{r}$$
Lagrangian is made of kinetic energy caluculated by these, i.e.
$$\frac{2}{m}L=A\dot{x}^2 + B\dot{x}+C$$
where
$$A=\sin^2\phi+\sec^2\phi=1+\frac{x^2}{r^2}+\frac{x^2}{r^2+x^2}$$
$$B=2r\Omega \sec^2\phi = 2r\Omega (1+\frac{x^2}{r^2}) $$
$$C=r^2\Omega^2 \sec^2\phi=r^2\Omega^2(1+\frac{x^2}{r^2})$$
Lagrange equation is
$$ 2A\ddot{x}+A'\dot{x}^2-C'=0$$
where prime means derivative by x.
$$ A'=2x [\frac{1}{r^2}+\frac{r^2}{(r^2+x^2)^2}]$$
$$ C'=2\Omega^2 x$$

This seems more complicated than that of OP.

In this equation x=0 is not singular point but it might be a stationary solution.

In a simple case of no wire, mass m is detatched from the disk at a moment and do intertial motion later. It also stands if the wire is attached. The wire extends as $x=r\Omega t$ and no tension in it. The time reversal of it also stands: m is approaching the disk. No tension in the winded wire. Here no show of potential energy.

T=0 means wire does nothing. m will do free inertial motion. $T\neq 0$ means that the wire would decrease $\Omega$ at the other end. Energy will be provided from outside of the system to maintain $\Omega$ so energy of mass should increase. If there is no potential, its kinetic energy should increase. I am not good at dealing with Lagrangian in such conditions.

 

[wrobel]

No given (active) forces, no potential energy, just ideal constraints.

Introduce a frame $Oxyz$. The axis $Oy$ passes through the point $O$ and the point where the string comes off the disk. The frame $Oxyz$ rotates and has the angular velocity
$$\boldsymbol \omega=(\Omega+\dot x/r)\boldsymbol e_z.$$
Kinetic energy of the system is
$$T=\frac{m}{2}|\boldsymbol v|^2,\quad \boldsymbol v=\frac{d}{dt}\boldsymbol{r}_m,$$
$$\boldsymbol{r}_m=x\boldsymbol e_x+r\boldsymbol e_y,$$
$$\boldsymbol v=\frac{d}{dt}\boldsymbol{r}_m=\dot x\boldsymbol e_x+x\boldsymbol\omega\times \boldsymbol e_x+r\boldsymbol\omega\times \boldsymbol e_y.$$
The Lagrangian is $L=T$. Up to a total derivative we finally obtain $L$ as I wrote above.

 

[wrobel]

No tension in the winded wire.

Once again: when we consider the mathematical pendulum we are not interested in whether the wire tightened or not. We consider an ideal constraint. Here is the same.

 

[anuttarasammyak]

I am sorry for my poor English. Tension force is zero. The wire outside the disk is straight and becomes short with pace $r\Omega$ during winding up operation around the disk bobbin.

Wire tension T is the only force acting on mass m so we need to know how it takes place. Does your Lagrangian help to understand it ?

 

[wrobel]

Wire tension T is the only force acting on mass m so we need to know how it takes place. Does your Lagrangian help to understand it ?

Sure. The Second Newton is $m\boldsymbol {\dot v}= \boldsymbol R.$ Here $\boldsymbol R =R\boldsymbol e_x$ stands for the tension force. The Lagrange equation in terms of the variable $\xi$ is trivially integrated and we can express $R$ as a function of $t$ and initial conditions.