To prove that three forces are in equilibrium

[gnits]

Homework Statement

To prove that three forces are in equilibrium

Relevant Equations

Equating of forces

Could I please ask for help regarding the following question:

D, E and F are the midpoints of the sides QR, RP and PQ respectively of triangle PQR whose circumcenter is O. Forces of magnitude kQR, kRP and kPQ act at O in directions $\overrightarrow{OD}$, $\overrightarrow{OE}$ and $\overrightarrow{OF}$ respectively.

Prove that the forces are in equilibrium.

I am allowed to make use of the following fact, (although I am free to answer the question any other way):

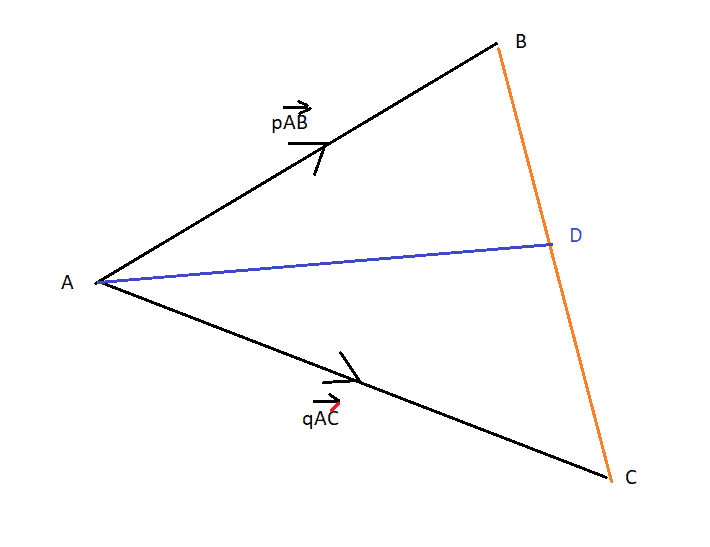
With both forces going away from A we have:

$p\overrightarrow{AB}$ + $q\overrightarrow{AC}$ = $(p+q)\overrightarrow{AD}$

where

$BD:DC = q:p$

Here's a diagram for the problem (the green stuff is referenced in my solution below where I attempt to apply the above fact).

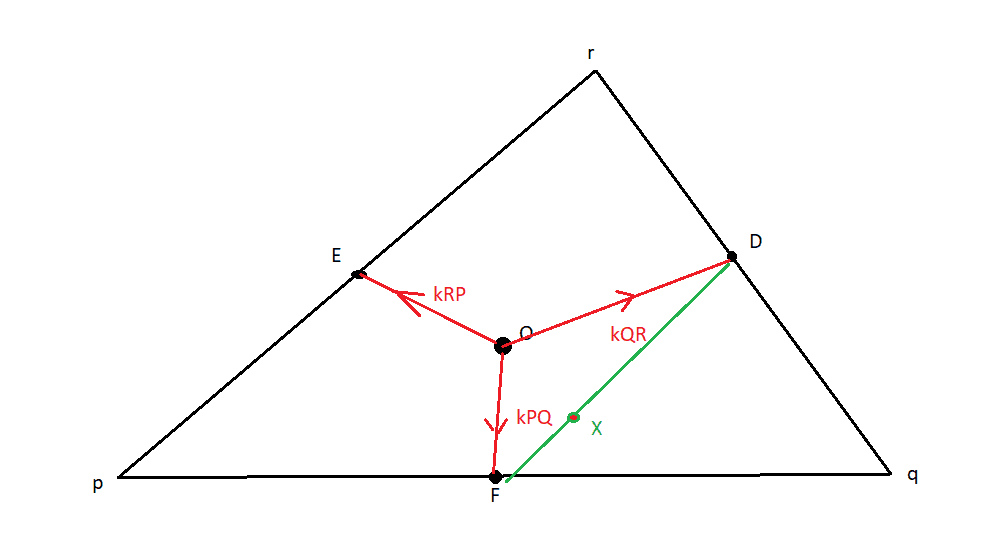
I was hoping to show that the kPQ and kQR forces combined to give a force which was opposite (so $\overrightarrow{OX}$ would be opposite to $\overrightarrow{OE}$ ) and of equal size to the kRP force by using the above fact. Well straight off I see that this would give a force of magnitude k(QR + PQ) which I would need to be equal to kRP, and I can't see how that can be so.

Thanks for any help,
Mitch.

 

[kuruman]

Can you show that the three forces form a closed triangle if you move them around parallel to themselves? Sure.

 

[gnits]

Can you show that the three forces form a closed triangle if you move them around parallel to themselves? Sure.

Thanks for your hint. I think it has enabled me to see it: I see that the three forces have lengths which are in the same proportion to each other as the original triangle,. Now, because O is the circumcentre then it must be the case that each of the forces is perpendicular to the side of the original triangle that it intersects (e.g. OD is perpendicular to rq etc). So the lines are of the right length and relative orientation to each other to form a closed triangle which is similar to the original. (Now, I doubt myself, D is the midpoint of rq, doesn't mean that OD is perpendicular to rq though). Ok, it does because O, being the circumcentre, is equidistant from r and q).

 

[kuruman]

Not quite.

Now, because O is the circumcentre then it must be the case that each of the forces is perpendicular to the side of the original triangle that it intersects (e.g. OD is perpendicular to rq etc).

I don't think that this true. The problem says that OD intersects rq at its midpoint. This doesn't necessarily make OD perpendicular to rq. It would be perpendicular if rq were the base of an isosceles triangle, pr=pq. We are not told that this is the case here. Hint: You can construct a triangle uniquely if you are given (a) one side and the two angles that it is part of, (b) two sides and the angle between them, (c) all three sides.

 

[mjc123]

O as the circumcentre must be equidistant from all the vertices. Thus ORQ is an isosceles triangle and OD is perpendicular to QR. D,O,P are not necessarily collinear. O is not the centroid. (It might help to redraw the diagram more accurately.)

 

[kuruman]

To @gnits:
Let me provide a most generous second hint, but before you proceed reading this post, please reread the hint in post #4, paying special attention to case (c).

Most generous second hint: Line segments $RP$, $PQ$ and $QR$ form a triangle if put together. Can lengths $kRP$, $kPQ$ and $kQR$ (where $k$ is a constant) also form a triangle if put together? Why or why not?

 

[gnits]

Thanks to everyone for their help, kuruman's was particularly of help to me, I am most grateful. These have helped me to see my way to the answer. Thanks again, Mitch.