How to calculate the magnitudes of three forces around a hexagon

[gnits]

Homework Statement

How to calculate the magnitudes of three forces around a hexagon

Relevant Equations

balance of forces and torques

Can anyone please help me with the following?

Three forces which act along the sides AB, BC and CD of a regular hexagon ABCDEF of side 2a, have a resultant which acts along DF. When a couple of 4Pa in the sense CBA is added in the plane of the hexagon, the resultant acts along CA. Find the magnitudes of the three froces in terms of P.

I call the three forces F1, F2 and F3 and here is my diagram:

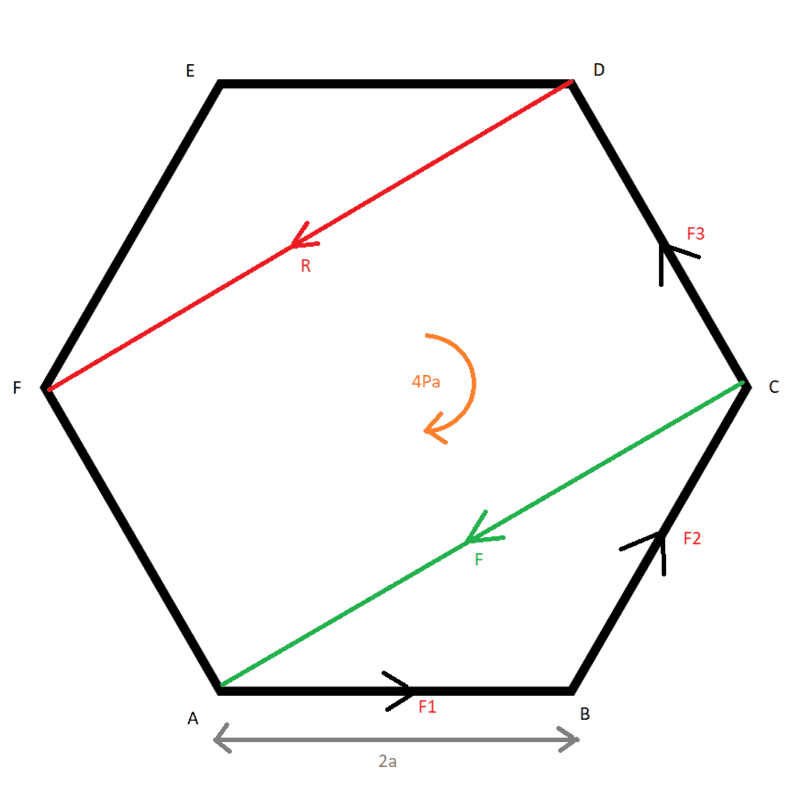
R is the resulatant of the three forces WITHOUT the torque.
F is the resultant of the three forces plus the torque.

answers given in book are:

F1 = 4P/sqrt(3)

F2 = -8P/sqrt(3)

F3 = 2*sqrt(3)P

I can find F1 by taking anitclockwise moments about C to give:

F1*sqrt(3)*a - 4*P*a = 0 and so F1 = 4*P / sqrt(3)

But I can't see how to find F2 and F3.

I can equate horizontal and vertical forces to get:

2*F1 + F2 - F3 = -sqrt(3)*F

and

sqrt(3)*F2 + sqrt(3)*F3 = -F

respectively.

I had hoped to substitute in my value for F1 to find F2 and F3 but that leads to these latter two equations reducing the same one.

I know that I somehow have to use the given fact that, after the torque is applied the resultant in parallel to the resultant prior to the torque being applied, but I can't see how.

Thanks for any help,
Mitch.

 

[haruspex]

use the given fact that, after the torque is applied the resultant in parallel to the resultant prior to the torque being applied

What force equation relates F and R?
What torque equation can you write from that?

 

[gnits]

What force equation relates F and R?
What torque equation can you write from that?

Thanks for the hints, but I still can't see my way to the solution. Given that F is R-plus-an-additionsal-pure-torque and that we a told that F is parallel to R then, in terms of forces, is not F = R? Given any relationship between F and R I am still unsure how I could form a torque equation between them (although I appreciate that such an equation would be another equation relating F1, F2 and F3 - which is what I need in order to solve).

Thanks again,
Mitch.

 

[haruspex]

in terms of forces, is not F = R?

Yes.

unsure how I could form a torque equation between them

Adding the torque to the one turned it into the other.

 

[Delta2]

Guys what do you mean adding the torque to one force turned it into the other. I tried reading the OP but i still can't understand: How can we add a torque and a force?

 

[jbriggs444]

Guys what do you mean adding the torque to one force turned it into the other. I tried reading the OP but i still can't understand: How can we add a torque and a force?

We are not exactly adding a torque and a force. We are adding a torque to a "force plus a line of action" to get a different "force plus a line of action". The idea is that if you take [almost] any pattern of forces and torques to a rigid object, you can get the equivalent effect with a single force applied along some line of action.

If the total magnitude of a force is $|\vec{R}|$ and one shifts the line of action of that force by a perpendicular offset of $2a$, what change in torque results?

 

[Delta2]

We are not exactly adding a torque and a force. We are adding a torque to a "force plus a line of action" to get a different "force plus a line of action". The idea is that if you take [almost] any pattern of forces and torques to a rigid object, you can get the equivalent effect with a single force applied along some line of action.

If the total magnitude of a force is $|\vec{R}|$ and one shifts the line of action of that force by a perpendicular offset of $2a$, what change in torque results?

Sorry, what exactly do you mean by "line of action" of a force?
if i understand correctly what it is, the change in torque is $2a|\vec{R}|$??

 

[jbriggs444]

Sorry, what exactly do you mean by "line of action" of a force?
if i understand correctly what it is, the change in torque is $2a|\vec{R}|$??

The "line of action" of a force is a line that is parallel to a force vector and which passes through the point where the force is applied. In the problem statement, the words "have a resultant which acts along DF" mean that DF is the "line of action" of the resultant equivalent force.

The effect of a force on a rigid object is completely determined by the force vector plus its line of action. Without knowing the line of action, you do not know how much torque is associated with the force.

 

[Delta2]

The "line of action" of a force is a line that is parallel to a force vector and which passes through the point where the force is applied.

The effect of a force on a rigid object is completely determined by the force vector plus its line of action

I don't understand what's the use of line of action , at least the way you define it, since by knowing the force vector we also know the line of action (parallel to force and passing through the point of application. Perhaps you meant to say the curve (and not necessarily a line) $\vec{r(t)}$ such that the torque of the force is $\vec{r(t)}\times \vec{F(t)}$

 

[jbriggs444]

I don't understand what's the use of line of action , at least the way you define it, since by knowing the force vector we also know the line of action (parallel to force and passing through the point of application. Perhaps you meant to say the curve (and not necessarily a line) $\vec{r(t)}$ such that the torque of the force is $\vec{r(t)}\times \vec{F(t)}$

The force vector by itself does not define the point of application.

 

[Delta2]

I think the OP is written with terminology used by mechanical engineers and not physicists/mathematicians, that's why I can't parse part of it.

 

[jbriggs444]

I think the OP is written with terminology used by mechanical engineers and not physicists/mathematicians, that's why I can't parse part of it.

I had considerable difficulty parsing it as well. I will try to translate...

Three forces which act along the sides AB, BC and CD of a regular hexagon ABCDEF of side 2a, have a resultant which acts along DF. When a couple of 4Pa in the sense CBA is added in the plane of the hexagon, the resultant acts along CA. Find the magnitudes of the three forces in terms of P.

We have a rigid regular hexagon.

Each of the sides is 2a in length. [Why the factor of 2 instead of just saying "r" in length and doing a change of variables, goodness knows].

The vertices of the hexagon are labelled "A" through "F" counter-clockwise.

Three forces are applied. One on side AB, one on side BC and one on side CD. The direction of each force is parallel [or anti-parallel] to the side where it is applied.

The sum of all three forces (the "resultant") $\vec{R}$ is parallel to side DF. The net torque on the hexagon resulting from the application of the three forces is identical to the torque on the hexagon if force $\vec{R}$ were applied at points D or F or anywhere else along that line.

If an additional clockwise pure torque (no associated net force) of magnitude $4Pa$ were applied together with the first three forces, the net effect on the hexagon would be the same as if force $\vec{R}$ were applied somewhere on line AC instead. [Again, with the silly constant multiples *sigh*]

We are asked to calculate the magnitudes of the three forces. We are expected to report them as positive if the forces are parallel to their respective sides and as negative if anti-parallel. We are expected to report them in terms of the unknown $P$.

Edit: Added "clockwise" and "counter-clockwise" designations to match the drawing. But the verbiage of the problem is also consistent with having both directions flipped.

 

[Delta2]

Thanks @jbriggs444 now i understand it almost 100%. Except one thing: Which is the point of reference with which we calculate torques?

 

[jbriggs444]

Thanks @jbriggs444 now i understand it almost 100%. Except one thing: Which is the point of reference with which we calculate torques?

It does not matter.

The notion of equivalent forces which I expect the poster is being trained and expected to use does not rely on a coordinate system or an origin about which to calculate torques. Using this scheme, a so-called "couple" is a pure torque. A "couple" is the equivalent of two equal and opposite forces applied at some non-zero offset from one another. Such a pair of forces yields the same net torque regardless of what point we choose to regard as the origin.

An object behaves as it behaves when subject to a combination of forces and couples, regardless of the coordinate system we choose to analyze that behavior.

[Personally, I've not been trained in this paradigm, but it seems entirely sound and compatible with a nice set of intuitions]

Edit: One might make a somewhat strained analogy with Thevenin and Norton equivalents in electronics.

One can always replace an arbitrary network of power sources (fixed potential differences), current sources (fixed current) and resistors between two terminals with an equivalent network consisting of a single power source and resistor in series (Thevenin) or a single current source and resistor in parallel (Norton).

The assignment of a reference zero potential is irrelevant.

 

[gnits]

Yes.

Adding the torque to the one turned it into the other.

Again, thanks very much for the help\hint, I'm just not seeing through to the solution. I get that if we take the force R which acts along DF and we add to it the clockwise torque 4Pa then the new resultant is equivalent to the force F of the along CA. I know that somehow that should give me an equation relating F1, F2 and F3 but I can't see how to form it.

Thanks,
Mitch.

 

[jbriggs444]

First things first.

Can you see how to compute the magnitude of F (and the magnitude of R as well since they are equal) based on the fact that changing the line of action by an offset of $2a$ changed the resulting torque by $4Pa$?

 

[haruspex]

Again, thanks very much for the help\hint, I'm just not seeing through to the solution. I get that if we take the force R which acts along DF and we add to it the clockwise torque 4Pa then the new resultant is equivalent to the force F of the along CA. I know that somehow that should give me an equation relating F1, F2 and F3 but I can't see how to form it.

Thanks,
Mitch.

Pick an axis - any axis, though some are more convenient than others. Compute the three torques about the axis and write the equation relating them. You will find that the choice of axis is immaterial, all choices producing the same equation.

 

[gnits]

First things first.

Can you see how to compute the magnitude of F (and the magnitude of R as well since they are equal) based on the fact that changing the line of action by an offset of $2a$ changed the resulting torque by $4Pa$?

Thanks jbriggs444 and haruspex for your hints and patience, I see it now and have the right answers. Thanks very much.