Topological Sort: Finding a Contradiction

[evinda]

Hello! (Wave)

The topological sort of a graph can be considered as an order of its nodes along a horizontal line so that all the directed edges go from the left to the right.

How could we show that all the directed edges go fom the left to the right?

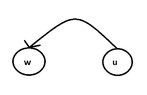
We suppose that it is:

View attachment 3843

Then it holds that $[d(w),f(w)] \subset [d(u),f(u)]$, right? (Thinking)

How could we find a contradiction?

 

[Evgeny.Makarov]

There is a distinction between a graph and its embedding in the plane. One cannot ask whether this vertex lies to the left of that vertex when talking about a graph, but this is a legitimate question about an embedding. The definition of the topological sort refers to a particular embedding of the given graph where all vertices lie on a line. It is possible to give an equivalent definition that does not refer to embeddings: simply require that there is a linear order $<$ on vertices such that the existence of an edge from $u$ to $v$ implies $u<v$.

Then it holds that $[d(w),f(w)] \subset [d(u),f(u)]$, right?

Could you explain the notation used in this formula?

 

[evinda]

Could you explain the notation used in this formula?

[m] d(u) [/m] is the discovery time of the node [m] u [/m], the first time we visit it.
[m] f(u) [/m] is the finishing time of the node [m] u [/m], the time when it can be considered discovered.

We find these values using the [m] DFS [/m] algorithm.

This the algorithm that it given for the topological sort:

TOPOLOGICALSORT(G)
1. Call DFS(G) to compute finishing times f(v),  for all v in V.
2. When a vertex is finished put it in front of a linked list.
3. return the linked list of vertices.